Collapsing manifold
Encyclopedia
In Riemannian geometry
, a collapsing or collapsed manifold is an n-dimensional manifold M that admits a sequence of Riemannian metrics
gn, such that as n goes to infinity the manifold is close to a k-dimensional space, where k < n, in the Gromov–Hausdorff distance sense. Generally there are some restrictions on the sectional curvatures of (M, gn). The simplest example is a flat manifold
, whose metric can be rescaled by 1/n, so that the manifold is close to a point, but its curvature remains 0 for all n.
(1) The first type is a collapse while keeping the curvature uniformly bounded, say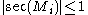
.
Let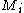
be a sequence of 
dimensional Riemannian manifolds, where 
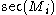denotes the sectional curvature of the ith manifold. There is a theorem proved by Jeff Cheeger
, Kenji Fukaya and Mikhail Gromov, which states that: There exists a constant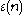
such that if 
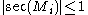and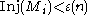 
, then 
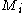admits an N-structure, with 
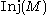denoting the injectivity radius of the manifold M. Roughly speaking the N-structure is a locally action of a nilmanifold
, which is a generalization of an F-structure, introduced by Cheeger and Gromov. This theorem generalized previous theorems of Cheeger-Gromov and Fukaya where they only deal with the torus action and bounded diameter cases respectively.
(2) The second type is the collapsing while keeping only the lower bound of curvature, say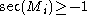
.
This is closely related to the so-called almost nonnegatively curved manifold case which generalizes non-negatively curved manifolds as well as almost flat manifolds. A manifold is said to be almost nonnegatively curved if it admits a sequence of metrics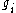
, such that 
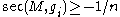and 
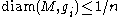. The role that an almost nonnegatively curved manifold plays in this collapsing case when curvature is bounded below is the same as an almost flat manifold plays in the curvature bounded case.
When curvature is only bounded below, the limit space is an Alexandrov space. A theorem says that on the regular part of the limit space, there is a fibration structure when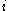
is sufficiently large, the fiber is an almost nonnegatively curved manifold. Here the regular means the 
-strainer radius is uniformly bounded from below by some number.
What happens at a singular point? There is no answer to this question at this time. But on dimension 3, Yamaguchi gives a full classification of this type collapsed manifold. He proved that there exists a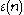
and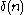 
such that if a 3-dimensional manifold 
satisfies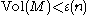 
then one of the following is true: (i) M is a graph manifold or (ii) 
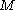has diameter less than 
and has finite fundamental group.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, a collapsing or collapsed manifold is an n-dimensional manifold M that admits a sequence of Riemannian metrics
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
gn, such that as n goes to infinity the manifold is close to a k-dimensional space, where k < n, in the Gromov–Hausdorff distance sense. Generally there are some restrictions on the sectional curvatures of (M, gn). The simplest example is a flat manifold
Flat manifold
In mathematics, a Riemannian manifold is said to be flat if its curvature is everywhere zero. Intuitively, a flat manifold is one that "locally looks like" Euclidean space in terms of distances and angles, e.g. the interior angles of a triangle add up to 180°....
, whose metric can be rescaled by 1/n, so that the manifold is close to a point, but its curvature remains 0 for all n.
Examples
Generally speaking there are two types of collapsing:(1) The first type is a collapse while keeping the curvature uniformly bounded, say
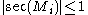.Let
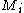be a sequence of dimensional Riemannian manifolds, where 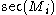denotes the sectional curvature of the ith manifold. There is a theorem proved by Jeff CheegerJeff Cheeger
Jeff Cheeger , is a mathematician. Cheeger is professor at the Courant Institute of Mathematical Sciences at New York University in New York City. His main interests are differential geometry and its applications to topology and analysis.-Biography:He graduated from Harvard University with a B.A....
, Kenji Fukaya and Mikhail Gromov, which states that: There exists a constant
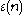such that if 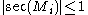and 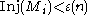, then 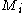admits an N-structure, with 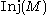denoting the injectivity radius of the manifold M. Roughly speaking the N-structure is a locally action of a nilmanifoldNilmanifold
In mathematics, a nilmanifold is a differentiable manifold which has a transitive nilpotent group of diffeomorphisms acting on it. As such, a nilmanifold is an example of a homogeneous space and is diffeomorphic to the quotient space N/H, the quotient of a nilpotent Lie group N modulo a closed...
, which is a generalization of an F-structure, introduced by Cheeger and Gromov. This theorem generalized previous theorems of Cheeger-Gromov and Fukaya where they only deal with the torus action and bounded diameter cases respectively.
(2) The second type is the collapsing while keeping only the lower bound of curvature, say
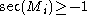.This is closely related to the so-called almost nonnegatively curved manifold case which generalizes non-negatively curved manifolds as well as almost flat manifolds. A manifold is said to be almost nonnegatively curved if it admits a sequence of metrics
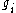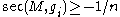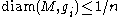, such that and . The role that an almost nonnegatively curved manifold plays in this collapsing case when curvature is bounded below is the same as an almost flat manifold plays in the curvature bounded case.When curvature is only bounded below, the limit space is an Alexandrov space. A theorem says that on the regular part of the limit space, there is a fibration structure when
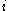is sufficiently large, the fiber is an almost nonnegatively curved manifold. Here the regular means the -strainer radius is uniformly bounded from below by some number.What happens at a singular point? There is no answer to this question at this time. But on dimension 3, Yamaguchi gives a full classification of this type collapsed manifold. He proved that there exists a
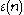and 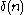such that if a 3-dimensional manifold satisfies 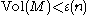then one of the following is true: (i) M is a graph manifold or (ii) 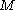has diameter less than and has finite fundamental group.