
Alternatization
Encyclopedia
In mathematics
, the notion of alternatization or alternatisation is used to pass from any map to an alternating map.
Let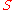 be a set and
be a set and  an Abelian group
an Abelian group
. Given a map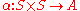 ,
,  is termed an alternating map if
is termed an alternating map if 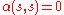 for all
for all 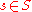 and
and 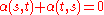 for all
for all 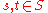 .
.
The alternatization of a general (not necessarily alternating) map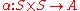 is the map
is the map 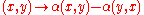 .
.
The alternatization of an alternating map is simply its double, while the alternatization of a symmetric map is zero.
The alternatization of a bilinear map is bilinear. There may be non-bilinear maps whose alternatization is also bilinear. Most notably, the alternatization of any cocycle
is bilinear. This fact plays a crucial role in identifying the second cohomology group of a lattice with the group of alternating bilinear forms on a lattice.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the notion of alternatization or alternatisation is used to pass from any map to an alternating map.
Let
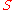 be a set and
be a set and  an Abelian group
an Abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. Given a map
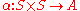 ,
,  is termed an alternating map if
is termed an alternating map if 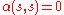 for all
for all 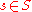 and
and 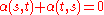 for all
for all 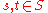 .
.The alternatization of a general (not necessarily alternating) map
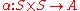 is the map
is the map 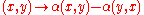 .
.The alternatization of an alternating map is simply its double, while the alternatization of a symmetric map is zero.
The alternatization of a bilinear map is bilinear. There may be non-bilinear maps whose alternatization is also bilinear. Most notably, the alternatization of any cocycle
Cocycle
A cocycle refers to any one of the following:*A closed cochain in algebraic topology is called a cocycle.*A particular type of map in an autonomous dynamical system; see Oseledec theorem....
is bilinear. This fact plays a crucial role in identifying the second cohomology group of a lattice with the group of alternating bilinear forms on a lattice.

