
Amalgamation property
Encyclopedia
In the mathematical field of model theory
, the amalgamation property is a property of collections of structures
that guarantees, under certain conditions, that two structures in the collection can be regarded as substructures of a larger one.
An amalgam can be formally defined as a 5-tuple (A,f,B,g,C) such that A,B,C are structures having the same signature
, and f: A → B, g: A → C are injective morphisms that are referred to as embeddings.
A class K of structures has the amalgamation property if for every amalgam with A,B,C ∈ K and A ≠ Ø, there exist both a structure D ∈ K and embeddings f': B → D, g': C → D such that
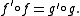
A simple example would be the class of sets with embeddings just being injective functions has the amalgamation property (with amalgam simply the union of the two sets). Another example would be the class of free group
s with embeddings being injective homomorphisms has the amalgamation property, where the amalgam is just the quotient group
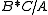 , where * is the free product
, where * is the free product
.
A notion in model theory that is similar to the amalgamation property (although different) is the joint embedding property
.
The diagram of the amalgamation property appears in many areas of mathematical logic. Examples include in modal logic
as an incestual accessibility relation, and in lambda calculus
as a manner of reduction having the Church-Rosser property.
': B → D, g': C → D such that

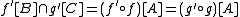

Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, the amalgamation property is a property of collections of structures
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
that guarantees, under certain conditions, that two structures in the collection can be regarded as substructures of a larger one.
An amalgam can be formally defined as a 5-tuple (A,f,B,g,C) such that A,B,C are structures having the same signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
, and f: A → B, g: A → C are injective morphisms that are referred to as embeddings.
A class K of structures has the amalgamation property if for every amalgam with A,B,C ∈ K and A ≠ Ø, there exist both a structure D ∈ K and embeddings f': B → D, g': C → D such that
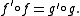
A simple example would be the class of sets with embeddings just being injective functions has the amalgamation property (with amalgam simply the union of the two sets). Another example would be the class of free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s with embeddings being injective homomorphisms has the amalgamation property, where the amalgam is just the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
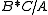 , where * is the free product
, where * is the free productFree product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
.
A notion in model theory that is similar to the amalgamation property (although different) is the joint embedding property
Joint embedding property
In universal algebra and model theory a class of structures K is said to have the joint embedding property if for all structures A and B in K there is a structure C in K such that both A and B are embeddable in C....
.
The diagram of the amalgamation property appears in many areas of mathematical logic. Examples include in modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
as an incestual accessibility relation, and in lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
as a manner of reduction having the Church-Rosser property.
Strong amalgamation property
A class K of structures has the strong amalgamation property (SAP) if for every amalgam with A,B,C ∈ K there exist both a structure D ∈ K and embeddings f
-
- and
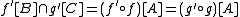
-
- where for any set X and function h on X,


