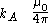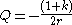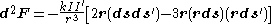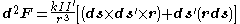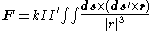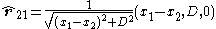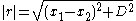
Ampère's force law
Encyclopedia
In magnetostatics
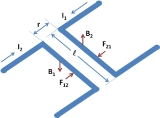
, the force of attraction or repulsion between two current-carrying wires (see Figure 1) is often called Ampère's force law. The physical origin of this force is that each wire generates a magnetic field, as defined by the Biot-Savart law
, and the other wire experiences a magnetic force as a consequence, as defined by the Lorentz force
.
The best-known and simplest example of Ampère's force law, which underlies the definition of the ampere
, the SI
unit of current, states that the force per unit length between two straight parallel conductors is
where kA is the magnetic force constant, r is the separation of the wires, and I1, I2 are the direct current
s carried by the wires. This is a good approximation for finite lengths if the distance between the wires is small compared to their lengths, but large compared to their diameters. The value of kA depends upon the system of units chosen, and the value of kA decides how large the unit of current will be. In the SI
system,
with μ0 the magnetic constant, defined in SI units as
Thus, in vacuum, the force per meter of length between two parallel conductors – spaced apart by 1 m and each carrying a current of 1 A
– is exactly
The general formulation of the magnetic force for arbitrary geometries is based on line integral
s and combines the Biot-Savart law
and Lorentz force
in one equation as shown below.
where
To determine the force between wires in a material medium, the magnetic constant is replaced by the actual permeability
of the medium.
. The x-component of the force between two linear currents I and I’, as depicted in the diagram to the right, was given by Ampere in 1825 and Gauss in 1833 as follows :
Following Ampere, a number of scientists, including Wilhelm Weber
, Rudolf Clausius
, James Clerk Maxwell
, Bernhard Riemann
and Walter Ritz
, developed this expression to find a fundamental expression of the force. Through differentiation, it can be shown that:
and also the identity:
With these expressions, Ampere's force law can be expressed as:
Using the identities:
and
Ampere's results can be expressed in the form:
As Maxwell noted, terms can be added to this expression, which are derivatives of a function Q(r) and, when integrated, cancel each other out. Thus, Maxwell gave "the most general form consistent with the experimental facts" for the force on ds arising from the action of ds' :
Q is a function of r, according to Maxwell, which "cannot be determined, without assumptions of some kind, from experiments in which the active current forms a closed circuit." Taking the function Q(r) to be of the form:
We obtain the general expression for the force exerted on ds by ds:
Integrating around s' eliminates k and the original expression given by Ampere and Gauss is obtained. Thus, as far as the original Ampere experiments are concerned, the value of k has no significance. Ampere took k=-1; Gauss took k=+1, as did Grassmann and Clausius, although Clausius omitted the S component. In the non-etheral electron theories, Weber took k=-1 and Riemann took k=+1. Ritz left k undetermined in his theory. If we take k = -1, we obtain the Ampere expression:
If we take k=+1, we obtain
Using the vector identity for the triple cross product, we may express this result as
When integrated around ds' the second term is zero, and thus we find the form of Ampere's force law given by Maxwell:
Assume wire 2 is along the x-axis, and wire 1 is at y=D, z=0, parallel to the x-axis. Let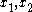
be the x-coordinate of the differential element of wire 1 and wire 2, respectively. In other words, the differential element of wire 1 is at 
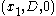and the differential element of wire 2 is at 
. By properties of line integrals, 
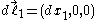and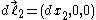 
. Also,
and
Therefore the integral is
Evaluating the cross-product:
Next, we integrate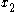
from 
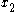to 
:
If wire 1 is also infinite, the integral diverges, because the total attractive force between two infinite parallel wires is infinity. In fact, we want to know the attractive force per unit length of wire 1. Therefore, assume wire 1 has a large but finite length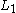
. Then the force vector felt by wire 1 is:
As expected, the force that the wire feels is proportional to its length. The force per unit length is:
The direction of the force is along the y-axis, representing wire 1 getting pulled towards wire 2 if the currents are parallel, as expected. The magnitude of the force per unit length agrees with the expression for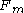
shown above.
Magnetostatics
Magnetostatics is the study of magnetic fields in systems where the currents are steady . It is the magnetic analogue of electrostatics, where the charges are stationary. The magnetization need not be static; the equations of magnetostatics can be used to predict fast magnetic switching events that...
, the force of attraction or repulsion between two current-carrying wires (see Figure 1) is often called Ampère's force law. The physical origin of this force is that each wire generates a magnetic field, as defined by the Biot-Savart law
Biot-Savart law
The Biot–Savart law is an equation in electromagnetism that describes the magnetic field B generated by an electric current. The vector field B depends on the magnitude, direction, length, and proximity of the electric current, and also on a fundamental constant called the magnetic constant...
, and the other wire experiences a magnetic force as a consequence, as defined by the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
.
The best-known and simplest example of Ampère's force law, which underlies the definition of the ampere
Ampere
The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics...
, the SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
unit of current, states that the force per unit length between two straight parallel conductors is
-
,
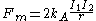where kA is the magnetic force constant, r is the separation of the wires, and I1, I2 are the direct current
Direct current
Direct current is the unidirectional flow of electric charge. Direct current is produced by such sources as batteries, thermocouples, solar cells, and commutator-type electric machines of the dynamo type. Direct current may flow in a conductor such as a wire, but can also flow through...
s carried by the wires. This is a good approximation for finite lengths if the distance between the wires is small compared to their lengths, but large compared to their diameters. The value of kA depends upon the system of units chosen, and the value of kA decides how large the unit of current will be. In the SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
system,
with μ0 the magnetic constant, defined in SI units as
-
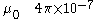newtons / (ampereAmpereThe ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics...
)2.
Thus, in vacuum, the force per meter of length between two parallel conductors – spaced apart by 1 m and each carrying a current of 1 A
Ampere
The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics...
– is exactly
-
-
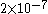N/m.
-
The general formulation of the magnetic force for arbitrary geometries is based on line integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
s and combines the Biot-Savart law
Biot-Savart law
The Biot–Savart law is an equation in electromagnetism that describes the magnetic field B generated by an electric current. The vector field B depends on the magnitude, direction, length, and proximity of the electric current, and also on a fundamental constant called the magnetic constant...
and Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
in one equation as shown below.
-
,
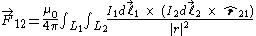where
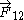is the total force felt by wire 1 due to wire 2 (usually measured in newtons),- I1 and I2 are the currents running through wires 1 and 2, respectively (usually measured in ampereAmpereThe ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics...
s), - The double line integration sums the force upon each element of wire 1 due to the magnetic field of each element of wire 2,
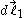and 
are infinitesimal vectors associated with wire 1 and wire 2 respectively (usually measured in metres); see line integralLine integralIn mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
for a detailed definition,- The vector
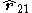is the unit vector pointing from the differential element on wire 2 towards the differential element on wire 1, and |r| is the distance separating these elements, - The multiplication × is a vector cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
, - The sign of In is relative to the orientation
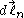(for example, if 
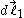points in the direction of conventional current, then I1>0).
To determine the force between wires in a material medium, the magnetic constant is replaced by the actual permeability
Permeability (electromagnetism)
In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...
of the medium.
Historical Background
The form of Ampere's force law commonly given was derived by Maxwell and is one of several expressions consistent with the original experiments of Ampere and GaussGauss
Gauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
. The x-component of the force between two linear currents I and I’, as depicted in the diagram to the right, was given by Ampere in 1825 and Gauss in 1833 as follows :
-
.
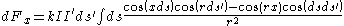Following Ampere, a number of scientists, including Wilhelm Weber
Wilhelm Eduard Weber
Wilhelm Eduard Weber was a German physicist and, together with Carl Friedrich Gauss, inventor of the first electromagnetic telegraph.-Early years:...
, Rudolf Clausius
Rudolf Clausius
Rudolf Julius Emanuel Clausius , was a German physicist and mathematician and is considered one of the central founders of the science of thermodynamics. By his restatement of Sadi Carnot's principle known as the Carnot cycle, he put the theory of heat on a truer and sounder basis...
, James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
, Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
and Walter Ritz
Walter Ritz
Walther Ritz was a Swiss theoretical physicist.His father, Raphael Ritz, a native of Valais, was a well-known landscape and interior scenes artist. His mother was the daughter of the engineer Noerdlinger of Tübingen. Ritz studied in Zurich and Göttingen...
, developed this expression to find a fundamental expression of the force. Through differentiation, it can be shown that:
-
.
and also the identity:
-
.
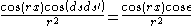With these expressions, Ampere's force law can be expressed as:
-
.
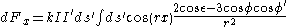Using the identities:
-
.
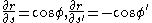and
-
.
Ampere's results can be expressed in the form:
-
.
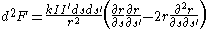As Maxwell noted, terms can be added to this expression, which are derivatives of a function Q(r) and, when integrated, cancel each other out. Thus, Maxwell gave "the most general form consistent with the experimental facts" for the force on ds arising from the action of ds' :
-
.
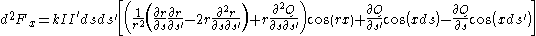Q is a function of r, according to Maxwell, which "cannot be determined, without assumptions of some kind, from experiments in which the active current forms a closed circuit." Taking the function Q(r) to be of the form:
We obtain the general expression for the force exerted on ds by ds:
-
.
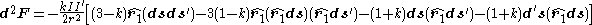Integrating around s' eliminates k and the original expression given by Ampere and Gauss is obtained. Thus, as far as the original Ampere experiments are concerned, the value of k has no significance. Ampere took k=-1; Gauss took k=+1, as did Grassmann and Clausius, although Clausius omitted the S component. In the non-etheral electron theories, Weber took k=-1 and Riemann took k=+1. Ritz left k undetermined in his theory. If we take k = -1, we obtain the Ampere expression:
If we take k=+1, we obtain
Using the vector identity for the triple cross product, we may express this result as
When integrated around ds' the second term is zero, and thus we find the form of Ampere's force law given by Maxwell:
Derivation of parallel straight wire case from general formula
Start from the general formula:-
,
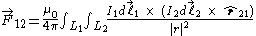Assume wire 2 is along the x-axis, and wire 1 is at y=D, z=0, parallel to the x-axis. Let
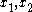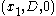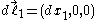be the x-coordinate of the differential element of wire 1 and wire 2, respectively. In other words, the differential element of wire 1 is at and the differential element of wire 2 is at . By properties of line integrals, and 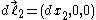. Also,
and
Therefore the integral is
-
.
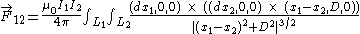Evaluating the cross-product:
-
.
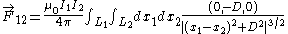Next, we integrate
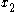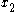from to :
-
.
If wire 1 is also infinite, the integral diverges, because the total attractive force between two infinite parallel wires is infinity. In fact, we want to know the attractive force per unit length of wire 1. Therefore, assume wire 1 has a large but finite length
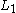. Then the force vector felt by wire 1 is:
-
.
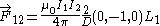As expected, the force that the wire feels is proportional to its length. The force per unit length is:
-
.
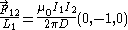The direction of the force is along the y-axis, representing wire 1 getting pulled towards wire 2 if the currents are parallel, as expected. The magnitude of the force per unit length agrees with the expression for
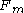shown above.Further reading
- Ampère's force law Includes animated graphic of the force vectors.
See also
- AmpereAmpereThe ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics...
- Magnetic constant
- Lorentz forceLorentz forceIn physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
- Ampère's circuital law
- Free space