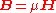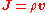
Biot-Savart law
Encyclopedia
The Biot–Savart law
is an equation in electromagnetism that describes the magnetic field
B generated by an electric current
. The vector field
B depends on the magnitude, direction, length, and proximity of the electric current, and also on a fundamental constant called the magnetic constant. The law is valid in the magnetostatic approximation
, and results in a B field consistent with both Ampère's circuital law and Gauss's law for magnetism.
generated by a steady current
, i.e. a continual flow of charges
, for example through a wire, which is constant in time and in which charge is neither building up nor depleting at any point. The equation in SI
units is
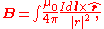
or, equivalently,
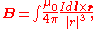
where
The symbols in boldface denote vector quantities.
To apply the equation, you choose a point in space at which you want to compute the magnetic field. Holding that point fixed, you integrate over the path of the current(s) to find the total magnetic field at that point. The application of this law implicitly relies on the superposition principle
for magnetic fields, i.e. the fact that the magnetic field is a vector sum of the field created by each infinitesimal section of the wire individually.
The formulations given above work well when the current can be approximated as running through an infinitely-narrow wire. If the current has some thickness, the proper formulation of the Biot–Savart law (again in SI
units) is:
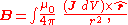or (equivalently),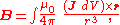 
where dV is the differential element of volume
and J is the current density
vector in that volume.
The Biot–Savart law is fundamental to magnetostatics
, playing a similar role to Coulomb's law
in electrostatics
. When magnetostatics does not apply, the Biot–Savart law should be replaced by Jefimenko's equations
.
, the magnetic field can be determined if the current density J is known:
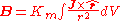
where:
is the differential element of volume.
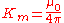is the magnetic constant
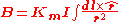
give the following expression for the electric field and magnetic field: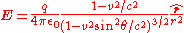
where
is the vector pointing from the current (non-retarded) position of the particle to the point at which the field is being measured, and θ is the angle between 
and 
.
When
, the electric field and magnetic field can be approximated as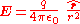
、
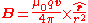
These equations are called the "Biot–Savart law for a point charge" due to its closely analogous form to the "standard" Biot–Savart law given previously. These equations were first derived by Oliver Heaviside
in 1888.
s or magnetic susceptibilities
, provided that the current density can be obtained from a quantum mechanical calculation or theory.
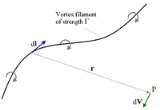
.png)
The Biot–Savart law is also used in aerodynamic theory to calculate the velocity induced by vortex lines
.
In the aerodynamic application, the roles of vorticity and current are reversed as when compared to the magnetic application.
In Maxwell's 1861 paper 'On Physical Lines of Force', magnetic field strength H was directly equated with pure vorticity (spin), whereas B was a weighted vorticity that was weighted for the density of the vortex sea. Maxwell considered magnetic permeability μ to be a measure of the density of the vortex sea. Hence the relationship,
(1) Magnetic induction current
was essentially a rotational analogy to the linear electric current relationship,
(2) Electric convection current
where ρ is electric charge density. B was seen as a kind of magnetic current of vortices aligned in their axial planes, with H being the circumferential velocity of the vortices.
The electric current equation can be viewed as a convective current of electric charge that involves linear motion. By analogy, the magnetic equation is an inductive current involving spin. There is no linear motion in the inductive current along the direction of the B vector. The magnetic inductive current represents lines of force. In particular, it represents lines of inverse square law force.
In aerodynamics the induced air currents are forming solenoidal rings around a vortex axis that is playing the role that electric current plays in magnetism. This puts the air currents of aerodynamics into the equivalent role of the magnetic induction vector B in electromagnetism.
In electromagnetism the B lines form solenoidal rings around the source electric current, whereas in aerodynamics, the air currents form solenoidal rings around the source vortex axis.
Hence in electromagnetism, the vortex plays the role of 'effect' whereas in aerodynamics, the vortex plays the role of 'cause'. Yet when we look at the B lines in isolation, we see exactly the aerodynamic scenario in so much as that B is the vortex axis and H is the circumferential velocity as in Maxwell's 1861 paper.
For a vortex line of infinite length, the induced velocity at a point is given by
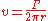
where
is the strength of the vortex
is the perpendicular distance between the point and the vortex line.
This is a limiting case of the formula for vortex segments of finite length:
where A and B are the (signed) angles between the line and the two ends of the segment.
{| class="toccolours collapsible collapsed" width="80%" style="text-align:left"
!Outline of proof that a magnetic field calculated by the Biot–Savart law will always satisfy Gauss's law for magnetism and Ampère's law.
|-
|Starting with the Biot–Savart law: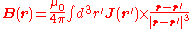
Plugging in the easily-derived relation
and using the product rule for curls, as well as the fact that J does not depend on the unprimed coordinates, this equation can be rewritten as
Since the divergence of a curl is always zero, this establishes Gauss's law for magnetism. Next, taking the curl of both sides, using the formula for the curl of a curl (see the article Curl (mathematics)), and again using the fact that J does not depend on the unprimed coordinates, we eventually get the result
Finally, plugging in the relations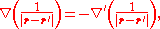
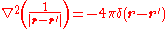
(where δ is the Dirac delta function
), using the fact that the divergence of J is zero (due to the assumption of magnetostatics
), and performing an integration by parts, the result turns out to be
i.e. Ampère's law.
|}
is an equation in electromagnetism that describes the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
B generated by an electric current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
. The vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
B depends on the magnitude, direction, length, and proximity of the electric current, and also on a fundamental constant called the magnetic constant. The law is valid in the magnetostatic approximation
Magnetostatics
Magnetostatics is the study of magnetic fields in systems where the currents are steady . It is the magnetic analogue of electrostatics, where the charges are stationary. The magnetization need not be static; the equations of magnetostatics can be used to predict fast magnetic switching events that...
, and results in a B field consistent with both Ampère's circuital law and Gauss's law for magnetism.
Introduction
The Biot–Savart law is used to compute the magnetic fieldMagnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
generated by a steady current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
, i.e. a continual flow of charges
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
, for example through a wire, which is constant in time and in which charge is neither building up nor depleting at any point. The equation in SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units is
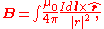
or, equivalently,
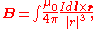
where
- I is the current,
- dl is a vector, whose magnitude is the length of the differentialInfinitesimalInfinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
element of the wire, and whose direction is the direction of conventional current, - B is the net magnetic field,
- μ0 is the magnetic constant,
is the displacement unit vector in the direction pointing from the wire element towards the point at which the field is being computed, and
is the full displacement vector from the wire element to the point at which the field is being computed.
The symbols in boldface denote vector quantities.
To apply the equation, you choose a point in space at which you want to compute the magnetic field. Holding that point fixed, you integrate over the path of the current(s) to find the total magnetic field at that point. The application of this law implicitly relies on the superposition principle
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
for magnetic fields, i.e. the fact that the magnetic field is a vector sum of the field created by each infinitesimal section of the wire individually.
The formulations given above work well when the current can be approximated as running through an infinitely-narrow wire. If the current has some thickness, the proper formulation of the Biot–Savart law (again in SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units) is:
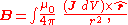or (equivalently),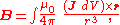 where dV is the differential element of volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
and J is the current density
Current density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
vector in that volume.
The Biot–Savart law is fundamental to magnetostatics
Magnetostatics
Magnetostatics is the study of magnetic fields in systems where the currents are steady . It is the magnetic analogue of electrostatics, where the charges are stationary. The magnetization need not be static; the equations of magnetostatics can be used to predict fast magnetic switching events that...
, playing a similar role to Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
in electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
. When magnetostatics does not apply, the Biot–Savart law should be replaced by Jefimenko's equations
Jefimenko's equations
In electromagnetism, Jefimenko's equations describe the behavior of the electric and magnetic fields in terms of the charge and current distributions at retarded times....
.
General
In the magnetostatic approximationMagnetostatics
Magnetostatics is the study of magnetic fields in systems where the currents are steady . It is the magnetic analogue of electrostatics, where the charges are stationary. The magnetization need not be static; the equations of magnetostatics can be used to predict fast magnetic switching events that...
, the magnetic field can be determined if the current density J is known:
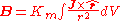
where:
is the differential element of volume.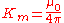 is the magnetic constantConstant uniform current
In the special case of a constant, uniform current I, the magnetic field B is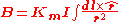Point charge at constant velocity
In the case of a charged point particle q moving at a constant velocity v, then Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
give the following expression for the electric field and magnetic field:
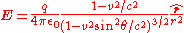
where
is the vector pointing from the current (non-retarded) position of the particle to the point at which the field is being measured, and θ is the angle between and .When
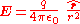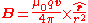
, the electric field and magnetic field can be approximated as 、These equations are called the "Biot–Savart law for a point charge" due to its closely analogous form to the "standard" Biot–Savart law given previously. These equations were first derived by Oliver Heaviside
Oliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
in 1888.
Magnetic responses applications
The Biot–Savart law can be used in the calculation of magnetic responses even at the atomic or molecular level, e.g. chemical shieldingChemical shift
In nuclear magnetic resonance spectroscopy, the chemical shift is the resonant frequency of a nucleus relative to a standard. Often the position and number of chemical shifts are diagnostic of the structure of a molecule...
s or magnetic susceptibilities
Magnetic susceptibility
In electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field...
, provided that the current density can be obtained from a quantum mechanical calculation or theory.
Aerodynamics applications
Vortex
A vortex is a spinning, often turbulent,flow of fluid. Any spiral motion with closed streamlines is vortex flow. The motion of the fluid swirling rapidly around a center is called a vortex...
.
In the aerodynamic application, the roles of vorticity and current are reversed as when compared to the magnetic application.
In Maxwell's 1861 paper 'On Physical Lines of Force', magnetic field strength H was directly equated with pure vorticity (spin), whereas B was a weighted vorticity that was weighted for the density of the vortex sea. Maxwell considered magnetic permeability μ to be a measure of the density of the vortex sea. Hence the relationship,
(1) Magnetic induction current
was essentially a rotational analogy to the linear electric current relationship,
(2) Electric convection current
where ρ is electric charge density. B was seen as a kind of magnetic current of vortices aligned in their axial planes, with H being the circumferential velocity of the vortices.
The electric current equation can be viewed as a convective current of electric charge that involves linear motion. By analogy, the magnetic equation is an inductive current involving spin. There is no linear motion in the inductive current along the direction of the B vector. The magnetic inductive current represents lines of force. In particular, it represents lines of inverse square law force.
In aerodynamics the induced air currents are forming solenoidal rings around a vortex axis that is playing the role that electric current plays in magnetism. This puts the air currents of aerodynamics into the equivalent role of the magnetic induction vector B in electromagnetism.
In electromagnetism the B lines form solenoidal rings around the source electric current, whereas in aerodynamics, the air currents form solenoidal rings around the source vortex axis.
Hence in electromagnetism, the vortex plays the role of 'effect' whereas in aerodynamics, the vortex plays the role of 'cause'. Yet when we look at the B lines in isolation, we see exactly the aerodynamic scenario in so much as that B is the vortex axis and H is the circumferential velocity as in Maxwell's 1861 paper.
For a vortex line of infinite length, the induced velocity at a point is given by
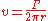
where
is the strength of the vortex is the perpendicular distance between the point and the vortex line.This is a limiting case of the formula for vortex segments of finite length:
where A and B are the (signed) angles between the line and the two ends of the segment.
The Biot–Savart law, Ampère's circuital law, and Gauss's law for magnetism
Here is a demonstration that the magnetic field B as computed from the Biot–Savart law will always satisfy Ampère's circuital law and Gauss's law for magnetism. Click "show" in the box below for an outline of the proof.{| class="toccolours collapsible collapsed" width="80%" style="text-align:left"
!Outline of proof that a magnetic field calculated by the Biot–Savart law will always satisfy Gauss's law for magnetism and Ampère's law.
|-
|Starting with the Biot–Savart law:
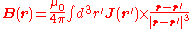
Plugging in the easily-derived relation
and using the product rule for curls, as well as the fact that J does not depend on the unprimed coordinates, this equation can be rewritten as
Since the divergence of a curl is always zero, this establishes Gauss's law for magnetism. Next, taking the curl of both sides, using the formula for the curl of a curl (see the article Curl (mathematics)), and again using the fact that J does not depend on the unprimed coordinates, we eventually get the result
Finally, plugging in the relations
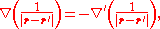
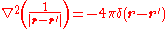
(where δ is the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
), using the fact that the divergence of J is zero (due to the assumption of magnetostatics
Magnetostatics
Magnetostatics is the study of magnetic fields in systems where the currents are steady . It is the magnetic analogue of electrostatics, where the charges are stationary. The magnetization need not be static; the equations of magnetostatics can be used to predict fast magnetic switching events that...
), and performing an integration by parts, the result turns out to be
i.e. Ampère's law.
|}
People
- Jean-Baptiste BiotJean-Baptiste BiotJean-Baptiste Biot was a French physicist, astronomer, and mathematician who established the reality of meteorites, made an early balloon flight, and studied the polarization of light.- Biography :...
- Félix SavartFélix SavartFélix Savart became a professor at Collège de France in 1836 and was the co-originator of the Biot-Savart Law, along with Jean-Baptiste Biot. Together, they worked on the theory of magnetism and electrical currents. Their law was developed about 1820. The Biot-Savart Law relates magnetic fields to...
- André-Marie AmpèreAndré-Marie AmpèreAndré-Marie Ampère was a French physicist and mathematician who is generally regarded as one of the main discoverers of electromagnetism. The SI unit of measurement of electric current, the ampere, is named after him....
- James Clerk MaxwellJames Clerk MaxwellJames Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
Electromagnetism
- Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
- Ampère's lawAmpère's lawIn classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
- MagnetismMagnetismMagnetism is a property of materials that respond at an atomic or subatomic level to an applied magnetic field. Ferromagnetism is the strongest and most familiar type of magnetism. It is responsible for the behavior of permanent magnets, which produce their own persistent magnetic fields, as well...
- Coulomb's lawCoulomb's lawCoulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
- Darwin Lagrangian
External links
- Electromagnetism, B. Crowell, Fullerton College
- MISN-0-125 The Ampère–Laplace–Biot–Savart Law by Orilla McHarris and Peter Signell for Project PHYSNET.