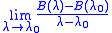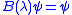In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the analytic Fredholm theorem is a result concerning the existence of bounded inverse

Inverse function

In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...

s for a family of bounded linear operators on a Hilbert space

Hilbert space

The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

. It is the basis of two classical and important theorems, the Fredholm alternative

Fredholm alternative

In mathematics, the Fredholm alternative, named after Ivar Fredholm, is one of Fredholm's theorems and is a result in Fredholm theory. It may be expressed in several ways, as a theorem of linear algebra, a theorem of integral equations, or as a theorem on Fredholm operators...

 and the Hilbert–Schmidt theorem. The result is named after the Swedish

Sweden

Sweden , officially the Kingdom of Sweden , is a Nordic country on the Scandinavian Peninsula in Northern Europe. Sweden borders with Norway and Finland and is connected to Denmark by a bridge-tunnel across the Öresund....

 mathematician

Mathematician

A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....

 Erik Ivar Fredholm

Erik Ivar Fredholm

Erik Ivar Fredholm was a Swedish mathematician who established the modern theory of integral equations. His 1903 paper in Acta Mathematica is considered to be one of the major landmarks in the establishment of operator theory.The lunar crater Fredholm is named after him.-List of publications:* E.I...

.

Statement of the theorem

Let G ⊆ C be a domain (an open

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

 and connected set

Connected space

In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...

). Let (H, ⟨ , ⟩) be a real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 or complex

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

 Hilbert space and let Lin(H) denote the space of bounded linear operators from H into itself; let I denote the identity operator. Let B : G → Lin(H) be a mapping such that

• B is analytic on G in the sense that that the limit
  Limit (mathematics)
  In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
  
  

exists for all λ₀ ∈ G; and

• the operator B(λ) is a compact operator
  Compact operator
  In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
  
   for each λ ∈ G.

Then either

• (I − B(λ))⁻¹ does not exist for any λ ∈ G; or

• (I − B(λ))⁻¹ exists for every λ ∈ G \ S, where S is a discrete subset of G (i.e., S has no limit point
  Limit point
  In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
  
  s in G). In this case, the function taking λ to (I − B(λ))⁻¹ is analytic on G \ S and, if λ ∈ S, then the equation

has a finite-dimensional family of solutions.