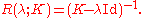Fredholm alternative
Encyclopedia
In mathematics
, the Fredholm alternative, named after Ivar Fredholm, is one of Fredholm's theorem
s and is a result in Fredholm theory
. It may be expressed in several ways, as a theorem of linear algebra
, a theorem of integral equation
s, or as a theorem on Fredholm operator
s. Part of the result states that a non-zero complex number in the spectrum
of a compact operator
is an eigenvalue.
and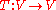 is a linear transformation
is a linear transformation
, then exactly one of the following holds:
A more elementary formulation, in terms of matrices, is as follows. Given an m×n matrix A and a m×1 column vector b, exactly one of the following must hold:
In other words, A x = b has a solution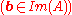 if and only if for any y s.t. AT y = 0, yTb = 0
if and only if for any y s.t. AT y = 0, yTb = 0  .
.
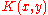 be an integral kernel, and consider the homogeneous equation
be an integral kernel, and consider the homogeneous equation
, the Fredholm integral equation
,
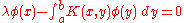
and the inhomogeneous equation
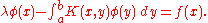
The Fredholm alternative states that, for any non-zero fixed complex number
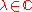 , either the first equation has a non-trivial solution, or the second equation has a solution for all
, either the first equation has a non-trivial solution, or the second equation has a solution for all  .
.
A sufficient condition for this theorem to hold is for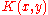 to be square integrable on the rectangle
to be square integrable on the rectangle  (where a and/or b may be minus or plus infinity).
(where a and/or b may be minus or plus infinity).
generalize these results to vector spaces of infinite dimensions, Banach space
s.
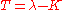
or, in index notation,

with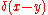 the Dirac delta function
the Dirac delta function
. Here, T can be seen to be an linear operator acting on a Banach space V of functions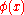 , so that
, so that

is given by

with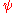 given by
given by

In this language, the integral equation alternatives are seen to correspond to the linear algebra alternatives.
. From Fredholm theory, smooth integral kernels are compact operators. The Fredholm alternative may be restated in the following form: a nonzero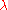 is either an eigenvalue of K, or it lies in the domain of the resolvent
is either an eigenvalue of K, or it lies in the domain of the resolvent
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Fredholm alternative, named after Ivar Fredholm, is one of Fredholm's theorem
Fredholm's theorem
In mathematics, Fredholm's theorems are a set of celebrated results of Ivar Fredholm in the Fredholm theory of integral equations. There are several closely related theorems, which may be stated in terms of integral equations, in terms of linear algebra, or in terms of the Fredholm operator on...
s and is a result in Fredholm theory
Fredholm theory
In mathematics, Fredholm theory is a theory of integral equations. In the narrowest sense, Fredholm theory concerns itself with the solution of the Fredholm integral equation. In a broader sense, the abstract structure of Fredholm's theory is given in terms of the spectral theory of Fredholm...
. It may be expressed in several ways, as a theorem of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a theorem of integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
s, or as a theorem on Fredholm operator
Fredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
s. Part of the result states that a non-zero complex number in the spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
of a compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
is an eigenvalue.
Linear algebra
If V is an n-dimensional vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
and
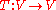 is a linear transformation
is a linear transformationLinear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
, then exactly one of the following holds:
- For each vector v in V there is a vector u in V so that
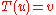 . In other words: T is surjective (and so also bijective, since V is finite-dimensional).
. In other words: T is surjective (and so also bijective, since V is finite-dimensional).  .
.
A more elementary formulation, in terms of matrices, is as follows. Given an m×n matrix A and a m×1 column vector b, exactly one of the following must hold:
- Either: A x = b has a solution x
- Or: AT y = 0 has a solution y with yTb ≠ 0.
In other words, A x = b has a solution
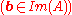 if and only if for any y s.t. AT y = 0, yTb = 0
if and only if for any y s.t. AT y = 0, yTb = 0  .
.Integral equations
Let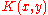 be an integral kernel, and consider the homogeneous equation
be an integral kernel, and consider the homogeneous equationHomogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
, the Fredholm integral equation
Fredholm integral equation
In mathematics, the Fredholm integral equation is an integral equation whose solution gives rise to Fredholm theory, the study of Fredholm kernels and Fredholm operators. The integral equation was studied by Ivar Fredholm.-Equation of the first kind :...
,
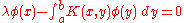
and the inhomogeneous equation
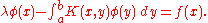
The Fredholm alternative states that, for any non-zero fixed complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
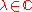 , either the first equation has a non-trivial solution, or the second equation has a solution for all
, either the first equation has a non-trivial solution, or the second equation has a solution for all  .
.A sufficient condition for this theorem to hold is for
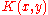 to be square integrable on the rectangle
to be square integrable on the rectangle  (where a and/or b may be minus or plus infinity).
(where a and/or b may be minus or plus infinity).Functional analysis
Results on the Fredholm operatorFredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
generalize these results to vector spaces of infinite dimensions, Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s.
Correspondence
Loosely speaking, the correspondence between the linear algebra version, and the integral equation version, is as follows: Let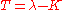
or, in index notation,

with
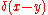 the Dirac delta function
the Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
. Here, T can be seen to be an linear operator acting on a Banach space V of functions
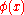 , so that
, so that
is given by

with
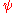 given by
given by
In this language, the integral equation alternatives are seen to correspond to the linear algebra alternatives.
Alternative
In more precise terms, the Fredholm alternative only applies when K is a compact operatorCompact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
. From Fredholm theory, smooth integral kernels are compact operators. The Fredholm alternative may be restated in the following form: a nonzero
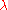 is either an eigenvalue of K, or it lies in the domain of the resolvent
is either an eigenvalue of K, or it lies in the domain of the resolventResolvent formalism
In mathematics, the resolvent formalism is a technique for applying concepts from complex analysis to the study of the spectrum of operators on Hilbert spaces and more general spaces....