
Ancestral relation
Encyclopedia
In mathematical logic
, the ancestral relation (often shortened to ancestral) of an arbitrary binary relation
R is defined below.
The ancestral makes its first appearance in Frege's Begriffsschrift
. Frege later employed it in his Grundgesetze as part of his definition of the natural number
s (actually the finite cardinals
). Hence the ancestral was a key part of his search for a logicist
foundation of arithmetic.
and recast in contemporary notation.
The property
F is "R-hereditary" if, whenever x is F and xRy, y is also F:
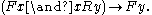
Frege then defined b to be an R-ancestor of a, written aR*b, iff
b has every R-hereditary property that all objects x such that aRx have:
76: .
.
The ancestral is transitive
:
98: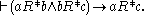
Let the notation I(R) denote that R is functional
(Frege calls such relations "many-one"):
115: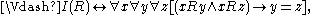
If R is functional
, we say nowadays that the ancestral of R is connected
:
133: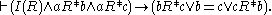
made repeated use of the ancestral, as does Quine's (1951) Mathematical Logic.
However, it is worth noting that the ancestral relation cannot be defined in first-order logic
, and following the resolution of Russell's paradox
both Frege and Quine largely considered the use of second-order logic
a questionable approach. In particular, Quine did not consider second-order logic to be "logic" at all, despite his reliance upon it for his 1951 book (which largely retells Principia in abbreviated form, for which second-order logic is required to fit its theorems).
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, the ancestral relation (often shortened to ancestral) of an arbitrary binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
R is defined below.
The ancestral makes its first appearance in Frege's Begriffsschrift
Begriffsschrift
Begriffsschrift is a book on logic by Gottlob Frege, published in 1879, and the formal system set out in that book...
. Frege later employed it in his Grundgesetze as part of his definition of the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s (actually the finite cardinals
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
). Hence the ancestral was a key part of his search for a logicist
Logicism
Logicism is one of the schools of thought in the philosophy of mathematics, putting forth the theory that mathematics is an extension of logic and therefore some or all mathematics is reducible to logic. Bertrand Russell and Alfred North Whitehead championed this theory fathered by Richard Dedekind...
foundation of arithmetic.
Definition
The numbered propositions below are taken from his BegriffsschriftBegriffsschrift
Begriffsschrift is a book on logic by Gottlob Frege, published in 1879, and the formal system set out in that book...
and recast in contemporary notation.
The property
Property (philosophy)
In modern philosophy, logic, and mathematics a property is an attribute of an object; a red object is said to have the property of redness. The property may be considered a form of object in its own right, able to possess other properties. A property however differs from individual objects in that...
F is "R-hereditary" if, whenever x is F and xRy, y is also F:
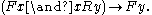
Frege then defined b to be an R-ancestor of a, written aR*b, iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
b has every R-hereditary property that all objects x such that aRx have:
76:
 .
.The ancestral is transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
:
98:
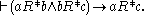
Let the notation I(R) denote that R is functional
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
(Frege calls such relations "many-one"):
115:
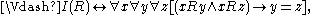
If R is functional
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, we say nowadays that the ancestral of R is connected
Connectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
:
133:
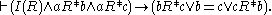
Discussion
Principia MathematicaPrincipia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
made repeated use of the ancestral, as does Quine's (1951) Mathematical Logic.
However, it is worth noting that the ancestral relation cannot be defined in first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, and following the resolution of Russell's paradox
Russell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
both Frege and Quine largely considered the use of second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
a questionable approach. In particular, Quine did not consider second-order logic to be "logic" at all, despite his reliance upon it for his 1951 book (which largely retells Principia in abbreviated form, for which second-order logic is required to fit its theorems).
External links
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
: "Frege's Logic, Theorem, and Foundations for Arithmetic" -- by Edward N. ZaltaEdward N. ZaltaEdward N. Zalta is a Senior research scholar at the Center for the Study of Language and Information. He received his Ph.D. in philosophy from the University of Massachusetts - Amherst in 1980. Zalta has taught courses at Stanford University, Rice University, the University of Salzburg, and the...
. Section 4.2.

