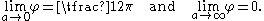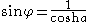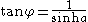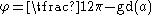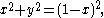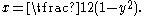
Angle of parallelism
Encyclopedia
In hyperbolic geometry
, the angle of parallelism φ, also known as Π(p), is the angle
at one vertex of a right hyperbolic triangle
that has two asymptotic parallel
sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism φ. Given a point off of a line, if we drop a perpendicular to the line from the point, then a is the distance along this perpendicular segment, and φ is the least angle such that the line drawn through the point at that angle does not intersect the given line. Since two sides are asymptotic parallel,
These five equivalent expressions relate φ and a:
where gd is the Gudermannian function.
 In the half-plane model of the hyperbolic plane (see hyperbolic motion
In the half-plane model of the hyperbolic plane (see hyperbolic motion
s) one can establish the relation of φ to a with Euclidean geometry
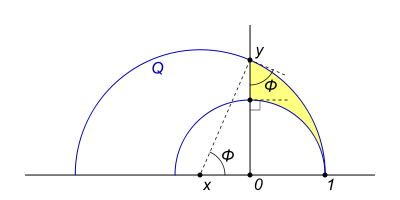
. Let Q be the semicircle with diameter on the x-axis that passes through the points (1,0) and (0,y), where y > 1. Since Q is tangent to the unit semicircle centered at the origin, the two semicircles represent parallel hyperbolic lines. The y-axis crosses both semicircles, making a right angle with the unit semicircle and a variable angle φ with Q. The angle at the center of Q subtended by the radius to (0, y) is also φ because the two angles have sides that are perpendicular, left side to left side, and right side to right side. The semicircle Q has its center at (x, 0), x < 0, so its radius is 1 − x. Thus, the radius squared of Q is
hence
The metric
of the half-plane model of hyperbolic geometry parametrizes distance on the ray {(0, y) : y > 0 } with natural logarithm
. Let log y = a, so y = ea. Then
the relation between φ and a can be deduced from the triangle {(x, 0), (0, 0), (0, y)}, for example:
:
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, the angle of parallelism φ, also known as Π(p), is the angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
at one vertex of a right hyperbolic triangle
Hyperbolic triangle
In mathematics, the term hyperbolic triangle has more than one meaning.-Hyperbolic geometry:In hyperbolic geometry, a hyperbolic triangle is a figure in the hyperbolic plane, analogous to a triangle in Euclidean geometry, consisting of three sides and three angles...
that has two asymptotic parallel
Limiting parallel
In neutral geometry, there may be many lines parallel to a given line l at a point P, however one parallel may be closer to l than all others. Thus it is useful to make a new definition concerning parallels in neutral geometry...
sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism φ. Given a point off of a line, if we drop a perpendicular to the line from the point, then a is the distance along this perpendicular segment, and φ is the least angle such that the line drawn through the point at that angle does not intersect the given line. Since two sides are asymptotic parallel,
These five equivalent expressions relate φ and a:
where gd is the Gudermannian function.
Demonstration

Hyperbolic motion
In geometry, hyperbolic motions are isometric automorphisms of a hyperbolic space. Under composition of mappings, the hyperbolic motions form a continuous group. This group is said to characterize the hyperbolic space. Such an approach to geometry was cultivated by Felix Klein in his Erlangen program...
s) one can establish the relation of φ to a with Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
. Let Q be the semicircle with diameter on the x-axis that passes through the points (1,0) and (0,y), where y > 1. Since Q is tangent to the unit semicircle centered at the origin, the two semicircles represent parallel hyperbolic lines. The y-axis crosses both semicircles, making a right angle with the unit semicircle and a variable angle φ with Q. The angle at the center of Q subtended by the radius to (0, y) is also φ because the two angles have sides that are perpendicular, left side to left side, and right side to right side. The semicircle Q has its center at (x, 0), x < 0, so its radius is 1 − x. Thus, the radius squared of Q is
hence
The metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
of the half-plane model of hyperbolic geometry parametrizes distance on the ray {(0, y) : y > 0 } with natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
. Let log y = a, so y = ea. Then
the relation between φ and a can be deduced from the triangle {(x, 0), (0, 0), (0, y)}, for example:
Lobachevsky originator
The following presentation in 1826 by Nicolai Lobachevsky is from the 1891 translation by G. B. HalstedG. B. Halsted
George Bruce Halsted was a mathematician who explored foundations of geometry and introduced Non-Euclidean geometry into the United States through his own work and his many important translations...
:
- The angle HAD between the parallel HA and the perpendicular AD is called the parallel angle (angle of parallelism) which we will here designate by Π(p) for AD = p
- see second appendix of Non-Euclidean Geometry by Roberto Bonola, Dover editionDover PublicationsDover Publications is an American book publisher founded in 1941 by Hayward Cirker and his wife, Blanche. It publishes primarily reissues, books no longer published by their original publishers. These are often, but not always, books in the public domain. The original published editions may be...
.
- see second appendix of Non-Euclidean Geometry by Roberto Bonola, Dover edition