
Anisotropic Network Model
Encyclopedia
The Anisotropic Network Model (ANM) is a simple yet powerful tool made for Normal Mode
Analysis of proteins, which has been successfully applied for exploring the relation between function and dynamics for many proteins. It is essentially an Elastic Network Model for the Cα atoms with a step function for the dependence of the force constants on the inter-particle distance.
(GNM) (Bahar et al., 1997; Haliloglu et al., 1997), and by the work of Hinsen (1998) who first demonstrated the validity of performing EN NMA at residue level.
It represents the biological macromolecule as an elastic mass-and-spring network (Figure.1.), to explain the internal motions of a protein subject to a harmonic potential. In the network each node is the Cα atom of the residue and the springs represent the interactions between the nodes. The overall potential is the sum of harmonic potentials between interacting nodes. To describe the internal motions of the spring connecting the two atoms, there is only one degree of freedom. Qualitatively, this corresponds to the compression and expansion of the spring in a direction given by the locations of the two atoms. In other words, ANM is an extension of the Gaussian Network Model to three coordinates per atom, thus accounting for directionality.
The network includes all interactions within a cutoff distance, which is the only predetermined parameter in the model. Information about the orientation of each interaction with respect to the global coordinates system is considered within the Force constant matrix (H) and allows prediction of anisotropic motions. Consider a sub-system consisting of nodes i and j, let ri = (xi yi zi) and let rj = (xj yj zj) be the instantaneous positions of atoms i and j. The equilibrium distance between the atoms is represented by sijO and the instantaneous distance is given by sij. For the spring between i and j, the harmonic potential in terms of the unknown spring constant γ, is given by:
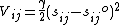
The second derivatives of the potential, Vij with respect to the components of ri are evaluated at the equilibrium position, i.e. sijO = sij, are
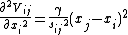
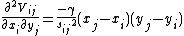
The force constant of the system can be described by the Hessian Matrix
– (second partial derivative of potential V):
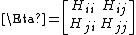
Each element Hi,j is a 3×3 matrix which holds the anisotropic information regarding the orientation of nodes i,j. Each such sub matrix (or the "super element" of the Hessian) is defined as:
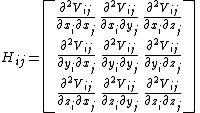
Using the definition of the potential, the Hessian can be expanded as,
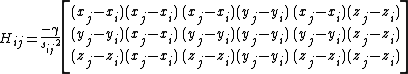
which can then be written as,
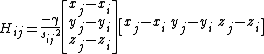
Here, the force constant matrix, or the hessian matrix H holds information about the orientation of the nodes, but not about the type of the interaction (such is whether the interaction is covalent or non-covalent, hydrophobic or non-hydrophobic, etc.). In addition, the distance between the interacting nodes is not considered directly. To account for the distance between the interactions we can weight each interaction between nodes i, j by the distance, sp. The new off-diagonal elements of the Hessian matrix take the below form, where p is an empirical parameter:
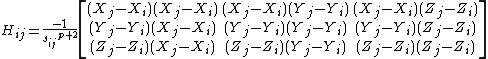
The counterpart of the Kirchhoff matrix Γ of the GNM is simply (1/γ) Η in the ANM. Its decomposition yields 3N - 6 non-zero eigenvalues, and 3N - 6 eigenvectors that reflect the respective frequencies and shapes of the individual modes. The inverse of Η, which holds the desired information about fluctuations is composed of N x N super-elements, each of which scales with the 3 x 3 matrix of correlations between the components of pairs of fluctuation vectors. The Hessian, however is not invertible, as its rank is 3N-6 (6 variables responsible to a rigid body motion). To obtain a pseudo inverse, a solution to the eigenvalue problem is obtained:
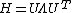
The pseudo-inverse is composed of the 3N-6 eigenvectors and their respective non-zero eigen values. Where λi are the eigenvalues of H sorted by their size from small to large and Ui the corresponding eigenvectors. The eigenvectors (the columns of the matrix U) describe the vibrational direction and the relative amplitude in the different modes.
It has been observed that GNM fluctuation predictions agree better with experiments than those computed with ANM. The higher performance of GNM can been attributed to its underlying potential, which takes account of orientational deformations, in addition to distance changes.
- ANM shows insensitivity to the choice of cutoff distance within a certain range, like GNM.
- Weighting the interactions by distance improves the correlation.
- Residue fluctuations in globular proteins are shown to be more accurately predicted, than those in non-globular proteins.
- Significant improvement in agreement with experiments is observed with increase in the resolution of the examined structure.
- While understanding how the accuracy of the predicted fluctuations is related to solvent accessibilities, the predictions for buried residues are shown to be in significantly better agreement with the experimental data as compared to the solvent-exposed ones.
- Polar/charged residues are more accurately predicted than hydrophobic ones, a possible consequence of the involvement of surface hydrophobic residues in crystal contacts.
- Hemoglobin
, by Chunyan et al., 2003.
- Influenza virus Hemagglutinin A, by Isin et al., 2002.
- Tubulin
, by Keskin et al., 2002.
- HIV-1 reverse transcriptase
complexed with different inhibitors, by Temiz and Bahar, 2002.
- HIV-1 protease
, by Micheletti et al., 2004; Vincenzo et al., 2006.
- DNA-polymerase, by Delarue and Sanejouand, 2002.
- Motor proteins, by Zheng and Brooks, 2005; Zheng and Brooks, 2005; Zheng and Doniach, 2003.
- Membrane proteins including potassium channels, by Shrivastava and Bahar, 2006.
- Rhodopsin
, by Rader et al., 2004.
- Nicotinic acetylcholine receptor
, by Hung et al., 2005; Taly et al., 2005 and a few more.
- Anisotropic Network Model web server. http://ignmtest.ccbb.pitt.edu/cgi-bin/anm/anm1.cgi
- ANM server. http://gor.bb.iastate.edu/anm/anm.htm
Normal mode
A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
Analysis of proteins, which has been successfully applied for exploring the relation between function and dynamics for many proteins. It is essentially an Elastic Network Model for the Cα atoms with a step function for the dependence of the force constants on the inter-particle distance.
Theory
The Anisotropic Network Model was introduced in 2000 (Atilgan et al., 2001; Doruker et al., 2000), inspired by the pioneering work of Tirion (1996), succeeded by the development of the Gaussian network modelGaussian network model
The Gaussian network model is a representation of a biological macromolecule as an elastic mass-and-spring network to study, understand, and characterize mechanical aspects of its long-scale dynamics...
(GNM) (Bahar et al., 1997; Haliloglu et al., 1997), and by the work of Hinsen (1998) who first demonstrated the validity of performing EN NMA at residue level.
It represents the biological macromolecule as an elastic mass-and-spring network (Figure.1.), to explain the internal motions of a protein subject to a harmonic potential. In the network each node is the Cα atom of the residue and the springs represent the interactions between the nodes. The overall potential is the sum of harmonic potentials between interacting nodes. To describe the internal motions of the spring connecting the two atoms, there is only one degree of freedom. Qualitatively, this corresponds to the compression and expansion of the spring in a direction given by the locations of the two atoms. In other words, ANM is an extension of the Gaussian Network Model to three coordinates per atom, thus accounting for directionality.
The network includes all interactions within a cutoff distance, which is the only predetermined parameter in the model. Information about the orientation of each interaction with respect to the global coordinates system is considered within the Force constant matrix (H) and allows prediction of anisotropic motions. Consider a sub-system consisting of nodes i and j, let ri = (xi yi zi) and let rj = (xj yj zj) be the instantaneous positions of atoms i and j. The equilibrium distance between the atoms is represented by sijO and the instantaneous distance is given by sij. For the spring between i and j, the harmonic potential in terms of the unknown spring constant γ, is given by:
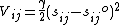
The second derivatives of the potential, Vij with respect to the components of ri are evaluated at the equilibrium position, i.e. sijO = sij, are
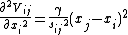
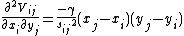
The force constant of the system can be described by the Hessian Matrix
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
– (second partial derivative of potential V):
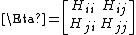
Each element Hi,j is a 3×3 matrix which holds the anisotropic information regarding the orientation of nodes i,j. Each such sub matrix (or the "super element" of the Hessian) is defined as:
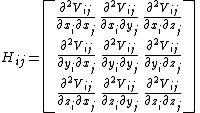
Using the definition of the potential, the Hessian can be expanded as,
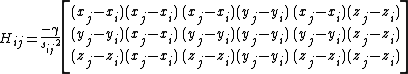
which can then be written as,
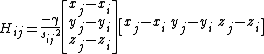
Here, the force constant matrix, or the hessian matrix H holds information about the orientation of the nodes, but not about the type of the interaction (such is whether the interaction is covalent or non-covalent, hydrophobic or non-hydrophobic, etc.). In addition, the distance between the interacting nodes is not considered directly. To account for the distance between the interactions we can weight each interaction between nodes i, j by the distance, sp. The new off-diagonal elements of the Hessian matrix take the below form, where p is an empirical parameter:
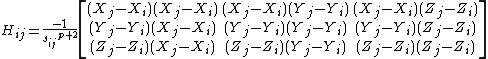
The counterpart of the Kirchhoff matrix Γ of the GNM is simply (1/γ) Η in the ANM. Its decomposition yields 3N - 6 non-zero eigenvalues, and 3N - 6 eigenvectors that reflect the respective frequencies and shapes of the individual modes. The inverse of Η, which holds the desired information about fluctuations is composed of N x N super-elements, each of which scales with the 3 x 3 matrix of correlations between the components of pairs of fluctuation vectors. The Hessian, however is not invertible, as its rank is 3N-6 (6 variables responsible to a rigid body motion). To obtain a pseudo inverse, a solution to the eigenvalue problem is obtained:
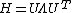
The pseudo-inverse is composed of the 3N-6 eigenvectors and their respective non-zero eigen values. Where λi are the eigenvalues of H sorted by their size from small to large and Ui the corresponding eigenvectors. The eigenvectors (the columns of the matrix U) describe the vibrational direction and the relative amplitude in the different modes.
Comparing ANM and GNM
ANM and GNM are both based on an elastic network model. The GNM has proven itself to accurately describe the vibrational dynamics of proteins and their complexes in numerous studies. Whereas the GNM is limited to the evaluation of the mean-square displacements and cross-correlations between fluctuations, the motion being projected to a mode space of N dimensions, the ANM approach permits us to evaluate directional preferences and thus provides 3-D descriptions of the 3N - 6 internal modes.It has been observed that GNM fluctuation predictions agree better with experiments than those computed with ANM. The higher performance of GNM can been attributed to its underlying potential, which takes account of orientational deformations, in addition to distance changes.
Evaluation of the Model
ANM has been evaluated on a large set of proteins to establish the optimal model parameters that achieve the highest correlation with experimental data and its limits of accuracy and applicability. The ANM is evaluated by comparing the fluctuations predicted from theory and those experimentally observed (B-factors deposited in the PDB). During evaluation, the following observations have been made about the models behavior.- ANM shows insensitivity to the choice of cutoff distance within a certain range, like GNM.
- Weighting the interactions by distance improves the correlation.
- Residue fluctuations in globular proteins are shown to be more accurately predicted, than those in non-globular proteins.
- Significant improvement in agreement with experiments is observed with increase in the resolution of the examined structure.
- While understanding how the accuracy of the predicted fluctuations is related to solvent accessibilities, the predictions for buried residues are shown to be in significantly better agreement with the experimental data as compared to the solvent-exposed ones.
- Polar/charged residues are more accurately predicted than hydrophobic ones, a possible consequence of the involvement of surface hydrophobic residues in crystal contacts.
Applications of ANM
Recent notable applications of ANM where it has proved to be a promising tool for describing the collective dynamics of the bio-molecular system, include the studies of:- Hemoglobin
Hemoglobin
Hemoglobin is the iron-containing oxygen-transport metalloprotein in the red blood cells of all vertebrates, with the exception of the fish family Channichthyidae, as well as the tissues of some invertebrates...
, by Chunyan et al., 2003.
- Influenza virus Hemagglutinin A, by Isin et al., 2002.
- Tubulin
Tubulin
Tubulin is one of several members of a small family of globular proteins. The most common members of the tubulin family are α-tubulin and β-tubulin, the proteins that make up microtubules. Each has a molecular weight of approximately 55 kiloDaltons. Microtubules are assembled from dimers of α- and...
, by Keskin et al., 2002.
- HIV-1 reverse transcriptase
Reverse transcriptase
In the fields of molecular biology and biochemistry, a reverse transcriptase, also known as RNA-dependent DNA polymerase, is a DNA polymerase enzyme that transcribes single-stranded RNA into single-stranded DNA. It also helps in the formation of a double helix DNA once the RNA has been reverse...
complexed with different inhibitors, by Temiz and Bahar, 2002.
- HIV-1 protease
HIV-1 protease
HIV-1 protease is a retroviral aspartyl protease that is essential for the life-cycle of HIV, the retrovirus that causes AIDS.HIV PR cleaves newly synthesized polyproteins at the appropriate places to create the mature protein components of an infectious HIV virion...
, by Micheletti et al., 2004; Vincenzo et al., 2006.
- DNA-polymerase, by Delarue and Sanejouand, 2002.
- Motor proteins, by Zheng and Brooks, 2005; Zheng and Brooks, 2005; Zheng and Doniach, 2003.
- Membrane proteins including potassium channels, by Shrivastava and Bahar, 2006.
- Rhodopsin
Rhodopsin
Rhodopsin, also known as visual purple, is a biological pigment of the retina that is responsible for both the formation of the photoreceptor cells and the first events in the perception of light. Rhodopsins belong to the G-protein coupled receptor family and are extremely sensitive to light,...
, by Rader et al., 2004.
- Nicotinic acetylcholine receptor
Nicotinic acetylcholine receptor
Nicotinic acetylcholine receptors, or nAChRs, are cholinergic receptors that form ligand-gated ion channels in the plasma membranes of certain neurons and on the postsynaptic side of the neuromuscular junction...
, by Hung et al., 2005; Taly et al., 2005 and a few more.
ANM Web Servers
The ANM web server developed by Eyal E, Yang LW, Bahar I. in 2006, presents a web-based interface for performing ANM calculations, the main strengths of which are the rapid computing ability and the user-friendly graphical capabilities for analyzing and interpreting the outputs.- Anisotropic Network Model web server. http://ignmtest.ccbb.pitt.edu/cgi-bin/anm/anm1.cgi
- ANM server. http://gor.bb.iastate.edu/anm/anm.htm

