Gaussian network model
Encyclopedia
The Gaussian network model (GNM) is a representation of a biological macromolecule
as an elastic mass-and-spring
network to study, understand, and characterize mechanical aspects of its long-scale dynamics
. The model has a wide range of applications from small proteins such as enzymes composed of a single domain
, to large macromolecular assemblies such as a ribosome
or a viral capsid
.
The Gaussian network model is a minimalist, coarse-grained approach to study biological molecules. In the model, proteins are represented by nodes corresponding to alpha carbons of the amino acid residues. Similarly, DNA and RNA structures are represented with one to three nodes for each nucleotide
. The model uses the harmonic approximation to model interactions, i.e. the spatial interactions between nodes (amino acids or nucleotides) are modeled with a uniform harmonic spring. This coarse-grained representation makes the calculations computationally inexpensive.
At molecular level, many biological phenomena, such as catalytic activity of an enzyme
, occur within the range of nano- to millisecond timescales. All atom simulation techniques, such as molecular dynamics
, rarely reach microsecond trajectory length, depending on the size of the system and accessible computational resources. Normal mode analysis in the context of GNM or elastic network (EN) models, in general, provides insights on the longer-scale functional behaviors of macromolecules. Here, the model captures native state functional motions of a biomolecule in the cost of atomic detail. The inference obtained from this model is complementary to atomic detail simulation techniques.
Another model for protein dynamics based on elastic mass-and-spring networks is the Anisotropic Network Model
.
The Gaussian network model was first proposed in 1996 by Tirion at the atomic level and then one year later reconsidered at the amino-acid level by Bahar, Atilgan, Haliloglu and Erman. The model was influenced by work of PJ Flory on polymer networks and other works that utilized normal mode analysis and simplified harmonic potentials to study dynamics of proteins.
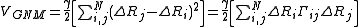
where γ is a force constant uniform for all springs and Γij is the ijth element of the Kirchhoff (or connectivity) matrix of inter-residue contacts, Γ, defined by
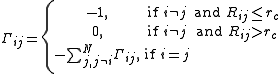
rc is a cutoff distance for spatial interactions and taken to be 7 Å for proteins.
Expressing the X, Y and Z components of the fluctuation vectors ΔRi as ΔXT = [ΔX1 ΔX2 ..... ΔXN], ΔYT = [ΔY1 ΔY2 ..... ΔYN], and ΔZT = [ΔZ1 ΔZ2 ..... ΔZN], above equation simplifies to
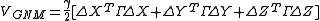
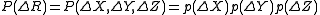
and Gaussian
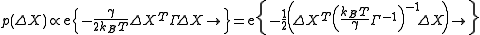
where kB is the Boltzmann constant and T is the absolute temperature. p(ΔY) and p(ΔZ) are expressed similarly.
N-dimensional Gaussian probability density function with random variable vector x, mean vector μ and covariance matrix Σ is
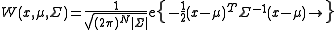
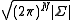normalizes the distribution and |Σ| is the determinant of the covariance matrix.
Similar to Gaussian distribution, normalized distribution for ΔXT = [ΔX1 ΔX2 ..... ΔXN] around the equilibrium positions can be expressed as
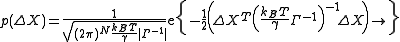
The normalization constant, also the partition function ZX, is given by
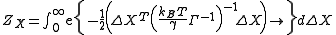
where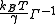
is the covariance matrix in this case. ZY and ZZ are expressed similarly. This formulation requires inversion of the Kirchhoff matrix. In the GNM, the determinant of the Kirchhoff matrix is zero, hence calculation of its inverse requires eigenvalue decomposition
. Γ−1 is constructed using the N-1 non-zero eigenvalues and associated eigenvectors. Expressions for p(ΔY) and p(ΔZ) are similar to that of p(ΔX). The probability distribution of all fluctuations in GNM becomes
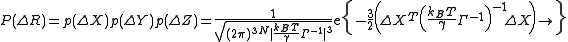
For this mass and spring system, the normalization constant in the preceding expression is the overall GNM partition function, ZGNM,
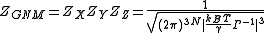
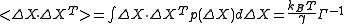
Since,
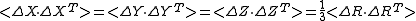
<ΔRi2> and <ΔRi · ΔRj> follows
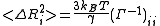
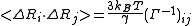
Cross-correlations between residue fluctuations can be written as a sum over the N-1 nonzero modes as
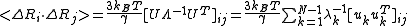
It follows that, [ΔRi · ΔRj], the contribution of an individual mode is expressed as
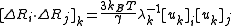
where [uk]i is the ith element of uk.
This expression shows that local packing density makes a significant contribution to expected fluctuations of residues. The terms that follow inverse of the diagonal matrix, are contributions of positional correlations to expected fluctuations.
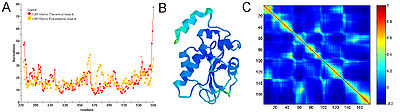
β-factor (or temperature factor) of each atom is a measure of mean-squared fluctuation of the native structure. In NMR experiments, this measure can be obtained by calculating root-mean-squared differences between different models.
In many applications and publications, including the original articles, it has been shown that expected residue fluctuations obtained from GNM is in good agreement with the experimentally measured native state fluctuations. The relation between b-factors, for example, and expected residue fluctuations obtained from GNM is as follows
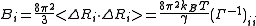
Figure 3 shows an example of GNM calculation for the catalytic domain of the protein Cdc25B, a cell division cycle dual-specifity phosphatase.
The first kind (the GNM per se) makes use of the Kirchhoff matrix. The second kind (more specifically called either the Elastic Network Model or the Anisotropic Network Model) makes use of the Hessian matrix
associated to the corresponding set of harmonic springs. Both kinds of models can be used online, using the following servers.
Macromolecule
A macromolecule is a very large molecule commonly created by some form of polymerization. In biochemistry, the term is applied to the four conventional biopolymers , as well as non-polymeric molecules with large molecular mass such as macrocycles...
as an elastic mass-and-spring
Spring (device)
A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...
network to study, understand, and characterize mechanical aspects of its long-scale dynamics
Dynamics (mechanics)
In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...
. The model has a wide range of applications from small proteins such as enzymes composed of a single domain
Protein domain
A protein domain is a part of protein sequence and structure that can evolve, function, and exist independently of the rest of the protein chain. Each domain forms a compact three-dimensional structure and often can be independently stable and folded. Many proteins consist of several structural...
, to large macromolecular assemblies such as a ribosome
Ribosome
A ribosome is a component of cells that assembles the twenty specific amino acid molecules to form the particular protein molecule determined by the nucleotide sequence of an RNA molecule....
or a viral capsid
Capsid
A capsid is the protein shell of a virus. It consists of several oligomeric structural subunits made of protein called protomers. The observable 3-dimensional morphological subunits, which may or may not correspond to individual proteins, are called capsomeres. The capsid encloses the genetic...
.
The Gaussian network model is a minimalist, coarse-grained approach to study biological molecules. In the model, proteins are represented by nodes corresponding to alpha carbons of the amino acid residues. Similarly, DNA and RNA structures are represented with one to three nodes for each nucleotide
Nucleotide
Nucleotides are molecules that, when joined together, make up the structural units of RNA and DNA. In addition, nucleotides participate in cellular signaling , and are incorporated into important cofactors of enzymatic reactions...
. The model uses the harmonic approximation to model interactions, i.e. the spatial interactions between nodes (amino acids or nucleotides) are modeled with a uniform harmonic spring. This coarse-grained representation makes the calculations computationally inexpensive.
At molecular level, many biological phenomena, such as catalytic activity of an enzyme
Enzyme
Enzymes are proteins that catalyze chemical reactions. In enzymatic reactions, the molecules at the beginning of the process, called substrates, are converted into different molecules, called products. Almost all chemical reactions in a biological cell need enzymes in order to occur at rates...
, occur within the range of nano- to millisecond timescales. All atom simulation techniques, such as molecular dynamics
Molecular dynamics
Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
, rarely reach microsecond trajectory length, depending on the size of the system and accessible computational resources. Normal mode analysis in the context of GNM or elastic network (EN) models, in general, provides insights on the longer-scale functional behaviors of macromolecules. Here, the model captures native state functional motions of a biomolecule in the cost of atomic detail. The inference obtained from this model is complementary to atomic detail simulation techniques.
Another model for protein dynamics based on elastic mass-and-spring networks is the Anisotropic Network Model
Anisotropic Network Model
The Anisotropic Network Model is a simple yet powerful tool made for Normal Mode Analysis of proteins, which has been successfully applied for exploring the relation between function and dynamics for many proteins...
.
Gaussian network model theory
The elastic network
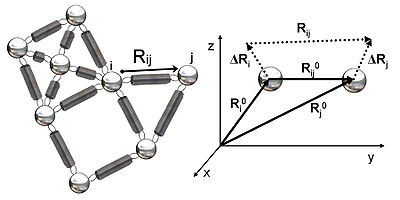
Figure 2 shows a schematic view of elastic network studied in GNM. Metal beads represent the nodes in this Gaussian network (residues of a protein) and springs represent the connections between the nodes of this network (covalent and non-covalent interactions between residues). For nodes i and j, equilibrium position vectors, R0i and R0j, equilibrium distance vector, R0ij, instantaneous fluctuation vectors, ΔRi and ΔRj, and instantaneous distance vector, Rij, are shown in Figure 2. Instantaneous position vectors of these nodes are defined by Ri and Rj. The difference between equilibrium position vector and instantaneous position vector of residue i gives the instantaneous fluctuation vector, ΔRi = Ri - R0i. Hence, the instantaneous fluctuation vector between nodes i and j is expressed as ΔRij = ΔRj - ΔRi = Rij - R0ij.Potential of the Gaussian network
Using the harmonic potential approximation, potential energy of the network in terms of ΔRi is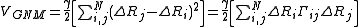where γ is a force constant uniform for all springs and Γij is the ijth element of the Kirchhoff (or connectivity) matrix of inter-residue contacts, Γ, defined by
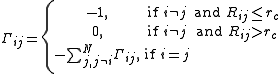
rc is a cutoff distance for spatial interactions and taken to be 7 Å for proteins.
Expressing the X, Y and Z components of the fluctuation vectors ΔRi as ΔXT = [ΔX1 ΔX2 ..... ΔXN], ΔYT = [ΔY1 ΔY2 ..... ΔYN], and ΔZT = [ΔZ1 ΔZ2 ..... ΔZN], above equation simplifies to
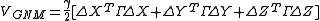
Statistical mechanics foundations
In the GNM, the probability distribution of all fluctuations, P(ΔR) is isotropic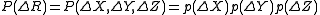and Gaussian
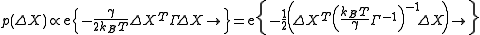
where kB is the Boltzmann constant and T is the absolute temperature. p(ΔY) and p(ΔZ) are expressed similarly.
N-dimensional Gaussian probability density function with random variable vector x, mean vector μ and covariance matrix Σ is
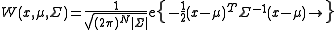
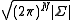normalizes the distribution and |Σ| is the determinant of the covariance matrix.Similar to Gaussian distribution, normalized distribution for ΔXT = [ΔX1 ΔX2 ..... ΔXN] around the equilibrium positions can be expressed as
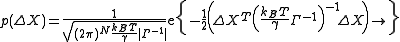
The normalization constant, also the partition function ZX, is given by
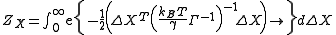
where
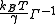is the covariance matrix in this case. ZY and ZZ are expressed similarly. This formulation requires inversion of the Kirchhoff matrix. In the GNM, the determinant of the Kirchhoff matrix is zero, hence calculation of its inverse requires eigenvalue decompositionSpectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
. Γ−1 is constructed using the N-1 non-zero eigenvalues and associated eigenvectors. Expressions for p(ΔY) and p(ΔZ) are similar to that of p(ΔX). The probability distribution of all fluctuations in GNM becomes
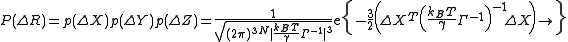
For this mass and spring system, the normalization constant in the preceding expression is the overall GNM partition function, ZGNM,
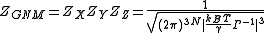
Expectation values of fluctuations and correlations
Based on the statistical mechanics foundations of GNM, expectation values of residue fluctuations, <ΔRi2> , and correlations, <ΔRi · ΔRj> , can be calculated. Covariance matrix for ΔX is given by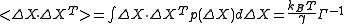Since,
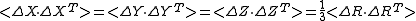
<ΔRi2> and <ΔRi · ΔRj> follows
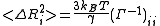
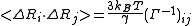
Mode decomposition
The GNM normal modes are found by diagonalization of the Kirchhoff matrix, Γ = UΛUT. Here, U is a unitary matrix, UT = U−1, of the eigenvectors ui of Γ and Λ is the diagonal matrix of eigenvalues λi. The frequency and shape of a mode is represented by its eigenvalue and eigenvector, respectively. Since the Kirchhoff matrix is positive semi-definite, the first eigenvalue, λ1, is zero and the corresponding eigenvector have all its elements equal to 1/√N. This shows that the network model is translation invariant.Cross-correlations between residue fluctuations can be written as a sum over the N-1 nonzero modes as
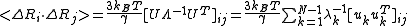
It follows that, [ΔRi · ΔRj], the contribution of an individual mode is expressed as
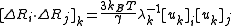
where [uk]i is the ith element of uk.
Influence of local packing density
By definition, a diagonal element of the Kirchhoff matrix, Γii, is equal to the degree of a node in GNM that represents the corresponding residue’s coordination number. This number is a measure of the local packing density around a given residue. The influence of local packing density can be assessed by series expansion of Γ−1 matrix. Γ can be written as a sum of two matrices, Γ = D + O, containing diagonal elements and off-diagonal elements of Γ.- Γ-1 = (D + O)-1 = [ D (I + D-1O) ]-1 = (I + D-1O)-1D-1 = (I - D-1O + ...)-1D-1 = D-1 - D-1O D-1 + ...
This expression shows that local packing density makes a significant contribution to expected fluctuations of residues. The terms that follow inverse of the diagonal matrix, are contributions of positional correlations to expected fluctuations.
GNM applications
Equilibrium fluctuations
Equilibrium fluctuations of biological molecules can be experimentally measured. In X-ray crystallographyX-ray crystallography
X-ray crystallography is a method of determining the arrangement of atoms within a crystal, in which a beam of X-rays strikes a crystal and causes the beam of light to spread into many specific directions. From the angles and intensities of these diffracted beams, a crystallographer can produce a...
β-factor (or temperature factor) of each atom is a measure of mean-squared fluctuation of the native structure. In NMR experiments, this measure can be obtained by calculating root-mean-squared differences between different models.
In many applications and publications, including the original articles, it has been shown that expected residue fluctuations obtained from GNM is in good agreement with the experimentally measured native state fluctuations. The relation between b-factors, for example, and expected residue fluctuations obtained from GNM is as follows
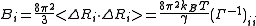
Figure 3 shows an example of GNM calculation for the catalytic domain of the protein Cdc25B, a cell division cycle dual-specifity phosphatase.
Physical meanings of slow and fast modes
Diagonalization of the Kirchhoff matrix decomposes the normal modes of collective motions of the Gaussian network model of a biomolecule. The expected values of fluctuations and cross-correlations are obtained from linear combinations of fluctuations along these normal modes. The contribution of each mode is scaled with the inverse of that modes frequency. Hence, slow (low frequency) modes contribute most to the expected fluctuations. Along the few slowest modes, motions are shown to be collective and global and potentially relevant to functionality of the biomolecules [9,13,15-18]. Fast (high frequency) modes, on the other hand, describe uncorrelated motions not inducing notable changes in the structure.Other specific applications
There are several major areas in which the Gaussian network model and other elastic network models are applied and found to be useful. These include:- Decomposition of flexible/rigid regions and domains of proteins
- Characterization of functional motions and functionally important sites/residues of proteins, enzymes and large macromolecular assemblies
- Refinement and dynamics of low-resolution structural data, e.g. Cryo-electron microscopyCryo-electron microscopyCryo-electron microscopy , or electron cryomicroscopy, is a form of transmission electron microscopy where the sample is studied at cryogenic temperatures...
- Molecular replacementMolecular replacementMolecular replacement is a method of solving the phase problem in X-ray crystallography. MR relies upon the existence of a previously solved protein structure which is homologous to our unknown structure from which the diffraction data is derived.The first goal of the crystallographer is to...
for solving X-ray structures, when a conformational changeConformational changeA macromolecule is usually flexible and dynamic. It can change its shape in response to changes in its environment or other factors; each possible shape is called a conformation, and a transition between them is called a conformational change...
occurred, with respect to a known structure - Integration with atomistic models and simulations
- Investigation of folding/unfolding pathways and kinetics.
- Annotation of functional implication in molecular evolution
Web servers
In practice, two kinds of calculations can be performed.The first kind (the GNM per se) makes use of the Kirchhoff matrix. The second kind (more specifically called either the Elastic Network Model or the Anisotropic Network Model) makes use of the Hessian matrix
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
associated to the corresponding set of harmonic springs. Both kinds of models can be used online, using the following servers.
GNM servers
- iGNM: A database of protein functional motions based on GNM http://ignm.ccbb.pitt.edu/Index.htm
- oGNM: Online calculation of structural dynamics using GNM http://ignm.ccbb.pitt.edu/GNM_Online_Calculation.htm
- GNM server http://gor.bb.iastate.edu/gnm/gnm.htm
ENM/ANM servers
- Anisotropic Network ModelAnisotropic Network ModelThe Anisotropic Network Model is a simple yet powerful tool made for Normal Mode Analysis of proteins, which has been successfully applied for exploring the relation between function and dynamics for many proteins...
web server http://www.ccbb.pitt.edu/anm - ANMAnisotropic Network ModelThe Anisotropic Network Model is a simple yet powerful tool made for Normal Mode Analysis of proteins, which has been successfully applied for exploring the relation between function and dynamics for many proteins...
server http://gor.bb.iastate.edu/anm/anm.htm - elNemo: Web-interface to The Elastic Network Model http://www.igs.cnrs-mrs.fr/elnemo/
- AD-ENM: Analysis of Dynamics of an Elastic Network Model http://enm.lobos.nih.gov/
- WEBnm@: Web-server for Normal Mode Analysis of proteins http://apps.cbu.uib.no/webnma/home
Other relevant servers
- ProMode: Database of normal mode analysis of proteins http://cube.socs.waseda.ac.jp/pages/jsp/index.jsp
- HingeProt: An algorithm for protein hinge prediction using elastic network models http://www.prc.boun.edu.tr/appserv/prc/hingeprot/, or http://bioinfo3d.cs.tau.ac.il/HingeProt/hingeprot.html
- MolMovDB: A database of macromolecular motions: http://www.molmovdb.org/
- The Protein Data BankProtein Data BankThe Protein Data Bank is a repository for the 3-D structural data of large biological molecules, such as proteins and nucleic acids....
(PDB) http://www.pdb.org/ - A comprephensive elastic network model server: http://omega.psi.iastate.edu
See also
- Gaussian distribution
- Harmonic oscillatorHarmonic oscillatorIn classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
- Hooke's lawHooke's lawIn mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
- Molecular dynamicsMolecular dynamicsMolecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
- Normal modeNormal modeA normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
- Principal component analysis
- Protein dynamics
- Rubber elasticityRubber ElasticityRubber elasticity, a well-known example of hyperelasticity, describes the mechanical behavior of many polymers, especially those with crosslinking. Invoking the theory of rubber elasticity, one considers a polymer chain in a crosslinked network as an entropic spring. When the chain is stretched,...
- Statistical mechanicsStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...