
Molecular replacement
Encyclopedia
Molecular replacement is a method of solving the phase problem
in X-ray crystallography
. MR relies upon the existence of a previously solved protein structure which is homologous (similar) to our unknown structure from which the diffraction data is derived.
The first goal of the crystallographer is to obtain an electron density map, density being related with diffracted wave as follows:

With usual detectors the intensity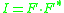 is being measured, so all the information about phase (
is being measured, so all the information about phase (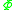 ) is lost.
) is lost.
Then, in the absence of phases (Φ), we are unable to complete the shown Fourier transform
relating the experimental data from X-ray crystallography
(in reciprocal space) to real-space electron density, into which the atomic model is built. MR tries to find the model which fits best experimental intensities among known structures.
, which is an interatomic vector map created by squaring the structure factor amplitudes and setting all phases to zero. This vector map contains a peak for each atom related to every other atom, with a large peak at 0,0,0, where vectors relating atoms to themselves "pile up". Such a map is far too noisy to derive any high resolution structural information—however if we generate Patterson maps for the data derived from our unknown structure, and from the structure of a previously solved homologue, in the correct orientation and position within the unit cell, the two Patterson maps should be closely correlated. This principle lies at the heart of MR, and can allow us to infer information about the orientation and location of an unknown molecule with its unit cell.
Due to historic limitations in computing power, an MR search is typically divided into two steps: rotation
and translation
.
were used to score the rotation function, however, modern programs use maximum likelihood
-based algorthims. The highest correlation (and therefore scores) are obtained when the two structures (known and unknown) are in similar orientation(s)—these can then be output in Euler angles
or spherical polar angles.
Phase problem
In physics the phase problem is the name given to the problem of loss of information concerning the phase that can occur when making a physical measurement. The name itself comes from the field of x-ray crystallography, where the phase problem has to be solved for the determination of a structure...
in X-ray crystallography
X-ray crystallography
X-ray crystallography is a method of determining the arrangement of atoms within a crystal, in which a beam of X-rays strikes a crystal and causes the beam of light to spread into many specific directions. From the angles and intensities of these diffracted beams, a crystallographer can produce a...
. MR relies upon the existence of a previously solved protein structure which is homologous (similar) to our unknown structure from which the diffraction data is derived.
The first goal of the crystallographer is to obtain an electron density map, density being related with diffracted wave as follows:

With usual detectors the intensity
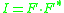 is being measured, so all the information about phase (
is being measured, so all the information about phase (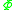 ) is lost.
) is lost.Then, in the absence of phases (Φ), we are unable to complete the shown Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
relating the experimental data from X-ray crystallography
X-ray crystallography
X-ray crystallography is a method of determining the arrangement of atoms within a crystal, in which a beam of X-rays strikes a crystal and causes the beam of light to spread into many specific directions. From the angles and intensities of these diffracted beams, a crystallographer can produce a...
(in reciprocal space) to real-space electron density, into which the atomic model is built. MR tries to find the model which fits best experimental intensities among known structures.
Principles of Patterson-based molecular replacement
However, we can derive a Patterson mapPatterson function
The Patterson function is used to solve the phase problem in X-ray crystallography. It was introduced in 1935 by Arthur Lindo Patterson while he was a visiting researcher in the laboratory of Bertram Eugene Warren at MIT....
, which is an interatomic vector map created by squaring the structure factor amplitudes and setting all phases to zero. This vector map contains a peak for each atom related to every other atom, with a large peak at 0,0,0, where vectors relating atoms to themselves "pile up". Such a map is far too noisy to derive any high resolution structural information—however if we generate Patterson maps for the data derived from our unknown structure, and from the structure of a previously solved homologue, in the correct orientation and position within the unit cell, the two Patterson maps should be closely correlated. This principle lies at the heart of MR, and can allow us to infer information about the orientation and location of an unknown molecule with its unit cell.
Due to historic limitations in computing power, an MR search is typically divided into two steps: rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
and translation
Translation
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. Whereas interpreting undoubtedly antedates writing, translation began only after the appearance of written literature; there exist partial translations of the Sumerian Epic of...
.
Rotation function
In the rotation function, our unknown Patterson map is compared to Patterson maps derived from our known homologue structure in different orientations. Historically r-factors and/or correlation coefficientsPearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
were used to score the rotation function, however, modern programs use maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
-based algorthims. The highest correlation (and therefore scores) are obtained when the two structures (known and unknown) are in similar orientation(s)—these can then be output in Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
or spherical polar angles.

