
Patterson function
Encyclopedia
The Patterson function is used to solve the phase problem
in X-ray crystallography
. It was introduced in 1935 by Arthur Lindo Patterson
(1902–1966) while he was a visiting researcher in the laboratory of Bertram Eugene Warren
(1902–1991) at MIT.
The Patterson function is defined as
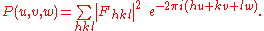
It is essentially the Fourier transform
of the intensities rather than the structure factor
s. The Patterson function is also equivalent to the electron density
convolved
with its inverse:
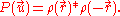
Furthermore, a Patterson map of N points will have N(N−1) peaks, excluding the central peak and any overlap.
The peaks in the Patterson function are the interatomic distance vectors weighted by the product of the number of electrons in the atoms concerned.
Because for each vector between atoms i and j there is an oppositely oriented vector of the same length (between atoms j and i), the Patterson function always has centrosymmetry
.
s given by
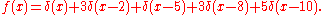
Then the Patterson function is

Phase problem
In physics the phase problem is the name given to the problem of loss of information concerning the phase that can occur when making a physical measurement. The name itself comes from the field of x-ray crystallography, where the phase problem has to be solved for the determination of a structure...
in X-ray crystallography
X-ray crystallography
X-ray crystallography is a method of determining the arrangement of atoms within a crystal, in which a beam of X-rays strikes a crystal and causes the beam of light to spread into many specific directions. From the angles and intensities of these diffracted beams, a crystallographer can produce a...
. It was introduced in 1935 by Arthur Lindo Patterson
Arthur Lindo Patterson
Arthur Lindo Patterson was a pioneering British X-ray crystallographer. Patterson was born to British parents in New Zealand in 1902. Shortly afterwards the family moved to Montreal, Canada and later to London, England. In 1920 Patterson moved to Canada for college at McGill University, Montreal...
(1902–1966) while he was a visiting researcher in the laboratory of Bertram Eugene Warren
Bertram Eugene Warren
Bertram Eugene Warren was an American crystallographer. His studies of X-rays provided much knowledge and understanding of both crystalline and non-crystalline materials. He also worked on changing amorphous solids to a crystalline state.-References:...
(1902–1991) at MIT.
The Patterson function is defined as
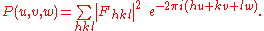
It is essentially the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the intensities rather than the structure factor
Structure factor
In condensed matter physics and crystallography, the static structure factor is a mathematical description of how a material scatters incident radiation...
s. The Patterson function is also equivalent to the electron density
Electron density
Electron density is the measure of the probability of an electron being present at a specific location.In molecules, regions of electron density are usually found around the atom, and its bonds...
convolved
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
with its inverse:
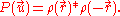
Furthermore, a Patterson map of N points will have N(N−1) peaks, excluding the central peak and any overlap.
The peaks in the Patterson function are the interatomic distance vectors weighted by the product of the number of electrons in the atoms concerned.
Because for each vector between atoms i and j there is an oppositely oriented vector of the same length (between atoms j and i), the Patterson function always has centrosymmetry
Centrosymmetry
The term centrosymmetric, as generally used in crystallography, refers to a space group which contains an inversion center as one of its symmetry elements. In such a space group, for every point in the unit cell there is an indistinguishable point...
.
One-dimensional example
Consider the series of delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
s given by
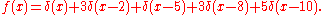
Then the Patterson function is



