
Ant on a rubber rope
Encyclopedia
Ant on a rubber rope is a mathematical puzzle
with a solution that appears counter-intuitive or paradoxical. It is sometimes given as a worm, or inchworm, on a rubber or elastic band, but the principles of the puzzle remain the same.
The details of the puzzle can vary,
but a typical form is as follows:
At first consideration it seems that the ant will never reach the end of the rope, but in fact it does (although in the form stated above the time taken is colossal). In fact, whatever the length of the rope and the relative speeds of the ant and the stretching, providing the ant's speed and the stretching remain steady the ant will always be able to reach the end given sufficient time.
 ), then it seems clear that the ant will reach the target-point (because it would eventually reach the target-point by walking along the axis, and walking along the rope can only carry it further forward).
), then it seems clear that the ant will reach the target-point (because it would eventually reach the target-point by walking along the axis, and walking along the rope can only carry it further forward).
Otherwise, we can still find a point on the rope that is receding at less than the speed of the ant on the rope by picking a suitable proportion of the distance from the starting-point to the target-point, e.g.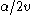 of the way along (any amount less than
of the way along (any amount less than 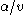 will work). Call this point
will work). Call this point 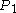 . It seems clear that the ant will reach
. It seems clear that the ant will reach 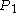 (because it would eventually reach
(because it would eventually reach  by walking along the axis, and walking along the rope can only carry it further forward). Now, the point on the rope at twice that proportion (call it
by walking along the axis, and walking along the rope can only carry it further forward). Now, the point on the rope at twice that proportion (call it 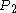 ) is receding at exactly the same speed from
) is receding at exactly the same speed from 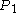 that
that 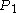 was receding from the starting-point (although it is by now rather further away). So the ant should be able to reach
was receding from the starting-point (although it is by now rather further away). So the ant should be able to reach 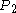 . And now, the point on the rope at three times the proportion (call it
. And now, the point on the rope at three times the proportion (call it 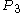 ) is receding at exactly the same speed from
) is receding at exactly the same speed from 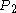 that
that 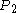 was receding from
was receding from 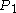 (although it is much further away). So the ant should be able to reach
(although it is much further away). So the ant should be able to reach 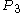 . This continues, and because the proportion of the way from the starting-point to the target-point at which each point,
. This continues, and because the proportion of the way from the starting-point to the target-point at which each point, 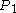 ,
, 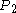 ,
, 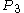 , etc., is found is a fixed amount greater than the proportion for the previous point, the proportion will eventually reach and exceed 1, so the ant will eventually reach the target-point.
, etc., is found is a fixed amount greater than the proportion for the previous point, the proportion will eventually reach and exceed 1, so the ant will eventually reach the target-point.
For the problem as originally stated, take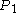 to be the point
to be the point 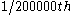 of the way along the rope. This point is travelling away from the starting-point at half the walking-speed of the ant, so the ant has no trouble reaching it. Point
of the way along the rope. This point is travelling away from the starting-point at half the walking-speed of the ant, so the ant has no trouble reaching it. Point 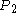 is
is 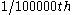 of the way along the rope and is travelling away from
of the way along the rope and is travelling away from  at half the walking-speed of the ant,
at half the walking-speed of the ant, 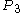 is
is 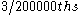 of the way along, etc., so after repeating the achievement 200,000 times the ant reaches the end of the rope. However, as the distance gets longer each time, so the time to complete each
of the way along, etc., so after repeating the achievement 200,000 times the ant reaches the end of the rope. However, as the distance gets longer each time, so the time to complete each 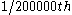 of the way gets longer each time, it is clear that the time required for the ant to complete the journey will be very large. This solution does not provide any more precise indication of how long it will take.
of the way gets longer each time, it is clear that the time required for the ant to complete the journey will be very large. This solution does not provide any more precise indication of how long it will take.
, originally in Scientific American
and later reprinted.
Consider a variation in which the rope stretches suddenly and instantaneously before each second, so that the target-point moves from to
to 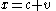 at time
at time 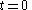 , and from
, and from 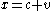 to
to 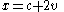 at time
at time 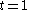 , etc. Many versions of the problem have the rope stretch at the end of each second, but by having the rope stretch before each second we have disadvantaged the ant in its goal, so we can be sure that if the ant can reach the target-point in this variation then it certainly can in the original problem or indeed in variants where the rope stretches at the end of each second.
, etc. Many versions of the problem have the rope stretch at the end of each second, but by having the rope stretch before each second we have disadvantaged the ant in its goal, so we can be sure that if the ant can reach the target-point in this variation then it certainly can in the original problem or indeed in variants where the rope stretches at the end of each second.
Let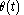 be the proportion of the distance from the starting-point to the target-point which the ant has covered at time t. So
be the proportion of the distance from the starting-point to the target-point which the ant has covered at time t. So 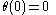 . In the first second the ant travels distance
. In the first second the ant travels distance 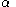 , which is
, which is 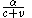 of the distance from the starting-point to the target-point (which is
of the distance from the starting-point to the target-point (which is 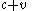 throughout the first second). When the rope stretches suddenly and instantaneously,
throughout the first second). When the rope stretches suddenly and instantaneously, 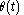 remains unchanged, because the ant moves along with the rubber where it is at that moment. So
remains unchanged, because the ant moves along with the rubber where it is at that moment. So 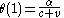 . In the next second the ant travels distance
. In the next second the ant travels distance 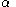 again, which is
again, which is 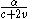 of the distance from the starting-point to the target-point (which is
of the distance from the starting-point to the target-point (which is 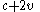 throughout that second). So
throughout that second). So 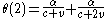 . Similarly, for any
. Similarly, for any 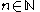 ,
, 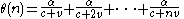 .
.
Notice that for any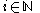 ,
, 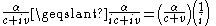 ,
,
so we can write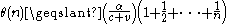 . The term
. The term 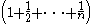 is a partial Harmonic series
is a partial Harmonic series
, which diverges
, so we can find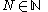 such that
such that 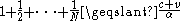 , which means that
, which means that 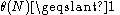 .
.
Therefore, given sufficient time, the ant will complete the journey to the target-point. This solution could be used to obtain an upper-bound for the time required, but does not give an exact answer for the time it will take.
 is its speed relative to the rope, i.e.
is its speed relative to the rope, i.e. 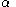 , plus the speed of the rope at the point where the ant is. The target-point moves with speed
, plus the speed of the rope at the point where the ant is. The target-point moves with speed 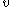 , so at time
, so at time  it is at
it is at 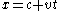 . Other points along the rope move with proportional speed, so at time
. Other points along the rope move with proportional speed, so at time  the point on the rope at
the point on the rope at 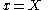 is moving with speed
is moving with speed 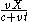 . So if we write the position of the ant at time
. So if we write the position of the ant at time  as
as 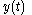 , and the speed of the ant at time
, and the speed of the ant at time  as
as 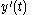 , we can write:
, we can write:
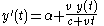
This is a first order linear differential equation, and it can be solved with standard methods. However, to do so requires some moderately advanced calculus. A much simpler approach considers the ant's position as a proportion of the distance from the starting-point to the target-point.
Consider coordinates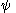 measured along the rope with the starting-point at
measured along the rope with the starting-point at 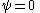 and the target-point at
and the target-point at 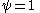 . In these coordinates, all points on the rope remain at a fixed position (in terms of
. In these coordinates, all points on the rope remain at a fixed position (in terms of 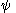 ) as the rope stretches. At time
) as the rope stretches. At time 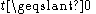 , a point at
, a point at 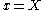 is at
is at 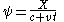 , and a speed
, and a speed 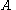 relative to the rope in terms of
relative to the rope in terms of 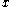 is equivalent to a speed
is equivalent to a speed  in terms of
in terms of  . So if we write the position of the ant in terms of
. So if we write the position of the ant in terms of 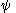 at time
at time  as
as 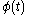 , and the speed of the ant in terms of
, and the speed of the ant in terms of 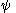 at time
at time  as
as 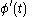 , we can write:
, we can write:
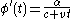
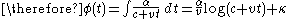 where
where 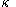 is a constant of integration.
is a constant of integration.
Now,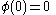 which gives
which gives 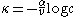 ,
,
so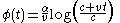 .
.
If the ant reaches the target-point (which is at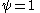 ) at time
) at time 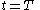 , we must have
, we must have 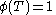 which gives us:
which gives us:
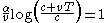
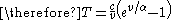
As this gives a finite value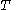 for all finite
for all finite  ,
, 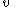 ,
, 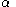 (
( ,
, 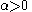 ), this means that, given sufficient time, the ant will complete the journey to the target-point. This formula can be used to find out how much time is required.
), this means that, given sufficient time, the ant will complete the journey to the target-point. This formula can be used to find out how much time is required.
For the problem as originally stated, ,
, 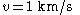 and
and 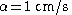 , which gives
, which gives 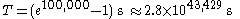 . This is a truly vast timespan, vast even in comparison to the estimated age of the universe, and the length of the rope after such a time is similarly huge, so it is only in a mathematical sense that the ant can ever reach the end of this particular rope.
. This is a truly vast timespan, vast even in comparison to the estimated age of the universe, and the length of the rope after such a time is similarly huge, so it is only in a mathematical sense that the ant can ever reach the end of this particular rope.
By thinking of light photons as ants crawling along the rubber rope of space between the galaxy and us, it can be seen that just as the ant will eventually reach the end of the rope, given sufficient time, so the light from the distant galaxy will eventually reach earth, given sufficient time.
Mathematical puzzle
Mathematical puzzles make up an integral part of recreational mathematics. They have specific rules as do multiplayer games, but they do not usually involve competition between two or more players. Instead, to solve such a puzzle, the solver must find a solution that satisfies the given conditions....
with a solution that appears counter-intuitive or paradoxical. It is sometimes given as a worm, or inchworm, on a rubber or elastic band, but the principles of the puzzle remain the same.
The details of the puzzle can vary,
but a typical form is as follows:
- An ant starts to crawl along a taut rubber rope 1 km long at a speed of 1 cm per second (relative to the rubber it is crawling on). At the same time, the rope starts to stretch by 1 km per second (so that after 1 second it is 2 km long, after 2 seconds it is 3 km long, etc). Will the ant ever reach the end of the rope?
At first consideration it seems that the ant will never reach the end of the rope, but in fact it does (although in the form stated above the time taken is colossal). In fact, whatever the length of the rope and the relative speeds of the ant and the stretching, providing the ant's speed and the stretching remain steady the ant will always be able to reach the end given sufficient time.
A formal statement of the problem
The problem as stated above requires some assumptions to be made. The following fuller statement of the problem attempts to make most of those assumptions explicit.- Consider a thin and infinitely stretchable rubber rope held taut along an
 -axis with a starting-point marked at
-axis with a starting-point marked at 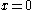 and a target-point marked at
and a target-point marked at  ,
, 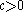 .
.
- At time
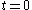 the rope starts to stretch uniformly and smoothly in such a way that the starting-point remains stationary at
the rope starts to stretch uniformly and smoothly in such a way that the starting-point remains stationary at 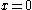 while the target-point moves away from the starting-point with constant speed
while the target-point moves away from the starting-point with constant speed 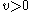 .
.
- A small ant leaves the starting-point at time
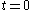 and walks steadily and smoothly along the rope towards the target-point at a constant speed
and walks steadily and smoothly along the rope towards the target-point at a constant speed 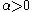 relative to the point on the rope where the ant is at each moment.
relative to the point on the rope where the ant is at each moment.
- Will the ant reach the target-point?
An informal reasoned solution
If the speed at which the target-point is receding from the starting-point is less than the speed of the ant on the rope (i.e., if ), then it seems clear that the ant will reach the target-point (because it would eventually reach the target-point by walking along the axis, and walking along the rope can only carry it further forward).
), then it seems clear that the ant will reach the target-point (because it would eventually reach the target-point by walking along the axis, and walking along the rope can only carry it further forward).Otherwise, we can still find a point on the rope that is receding at less than the speed of the ant on the rope by picking a suitable proportion of the distance from the starting-point to the target-point, e.g.
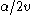 of the way along (any amount less than
of the way along (any amount less than 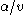 will work). Call this point
will work). Call this point 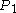 . It seems clear that the ant will reach
. It seems clear that the ant will reach 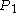 (because it would eventually reach
(because it would eventually reach  by walking along the axis, and walking along the rope can only carry it further forward). Now, the point on the rope at twice that proportion (call it
by walking along the axis, and walking along the rope can only carry it further forward). Now, the point on the rope at twice that proportion (call it 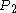 ) is receding at exactly the same speed from
) is receding at exactly the same speed from 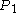 that
that 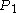 was receding from the starting-point (although it is by now rather further away). So the ant should be able to reach
was receding from the starting-point (although it is by now rather further away). So the ant should be able to reach 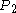 . And now, the point on the rope at three times the proportion (call it
. And now, the point on the rope at three times the proportion (call it 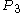 ) is receding at exactly the same speed from
) is receding at exactly the same speed from 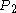 that
that 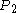 was receding from
was receding from 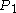 (although it is much further away). So the ant should be able to reach
(although it is much further away). So the ant should be able to reach 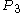 . This continues, and because the proportion of the way from the starting-point to the target-point at which each point,
. This continues, and because the proportion of the way from the starting-point to the target-point at which each point, 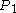 ,
, 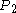 ,
, 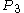 , etc., is found is a fixed amount greater than the proportion for the previous point, the proportion will eventually reach and exceed 1, so the ant will eventually reach the target-point.
, etc., is found is a fixed amount greater than the proportion for the previous point, the proportion will eventually reach and exceed 1, so the ant will eventually reach the target-point.For the problem as originally stated, take
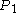 to be the point
to be the point 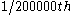 of the way along the rope. This point is travelling away from the starting-point at half the walking-speed of the ant, so the ant has no trouble reaching it. Point
of the way along the rope. This point is travelling away from the starting-point at half the walking-speed of the ant, so the ant has no trouble reaching it. Point 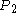 is
is 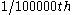 of the way along the rope and is travelling away from
of the way along the rope and is travelling away from  at half the walking-speed of the ant,
at half the walking-speed of the ant, 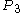 is
is 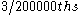 of the way along, etc., so after repeating the achievement 200,000 times the ant reaches the end of the rope. However, as the distance gets longer each time, so the time to complete each
of the way along, etc., so after repeating the achievement 200,000 times the ant reaches the end of the rope. However, as the distance gets longer each time, so the time to complete each 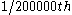 of the way gets longer each time, it is clear that the time required for the ant to complete the journey will be very large. This solution does not provide any more precise indication of how long it will take.
of the way gets longer each time, it is clear that the time required for the ant to complete the journey will be very large. This solution does not provide any more precise indication of how long it will take.A discrete mathematics solution
Although solving the problem appears to require analytical techniques, it can actually be answered by a combinatorial argument by considering a variation in which the rope stretches suddenly and instantaneously each second rather than stretching continuously. Indeed, the problem is sometimes stated in these terms, and the following argument is a generalisation of one set out by Martin GardnerMartin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
, originally in Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
and later reprinted.
Consider a variation in which the rope stretches suddenly and instantaneously before each second, so that the target-point moves from
 to
to 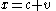 at time
at time 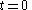 , and from
, and from 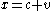 to
to 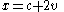 at time
at time 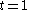 , etc. Many versions of the problem have the rope stretch at the end of each second, but by having the rope stretch before each second we have disadvantaged the ant in its goal, so we can be sure that if the ant can reach the target-point in this variation then it certainly can in the original problem or indeed in variants where the rope stretches at the end of each second.
, etc. Many versions of the problem have the rope stretch at the end of each second, but by having the rope stretch before each second we have disadvantaged the ant in its goal, so we can be sure that if the ant can reach the target-point in this variation then it certainly can in the original problem or indeed in variants where the rope stretches at the end of each second.Let
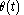 be the proportion of the distance from the starting-point to the target-point which the ant has covered at time t. So
be the proportion of the distance from the starting-point to the target-point which the ant has covered at time t. So 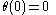 . In the first second the ant travels distance
. In the first second the ant travels distance 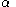 , which is
, which is 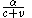 of the distance from the starting-point to the target-point (which is
of the distance from the starting-point to the target-point (which is 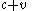 throughout the first second). When the rope stretches suddenly and instantaneously,
throughout the first second). When the rope stretches suddenly and instantaneously, 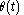 remains unchanged, because the ant moves along with the rubber where it is at that moment. So
remains unchanged, because the ant moves along with the rubber where it is at that moment. So 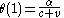 . In the next second the ant travels distance
. In the next second the ant travels distance 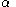 again, which is
again, which is 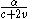 of the distance from the starting-point to the target-point (which is
of the distance from the starting-point to the target-point (which is 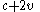 throughout that second). So
throughout that second). So 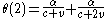 . Similarly, for any
. Similarly, for any 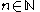 ,
, 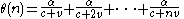 .
.Notice that for any
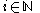 ,
, 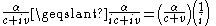 ,
,so we can write
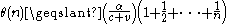 . The term
. The term 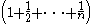 is a partial Harmonic series
is a partial Harmonic seriesHarmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
, which diverges
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
, so we can find
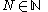 such that
such that 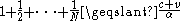 , which means that
, which means that 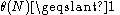 .
.Therefore, given sufficient time, the ant will complete the journey to the target-point. This solution could be used to obtain an upper-bound for the time required, but does not give an exact answer for the time it will take.
An analytical solution
A key observation is that the speed of the ant at a given time is its speed relative to the rope, i.e.
is its speed relative to the rope, i.e. 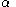 , plus the speed of the rope at the point where the ant is. The target-point moves with speed
, plus the speed of the rope at the point where the ant is. The target-point moves with speed 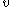 , so at time
, so at time  it is at
it is at 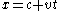 . Other points along the rope move with proportional speed, so at time
. Other points along the rope move with proportional speed, so at time  the point on the rope at
the point on the rope at 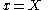 is moving with speed
is moving with speed 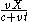 . So if we write the position of the ant at time
. So if we write the position of the ant at time  as
as 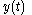 , and the speed of the ant at time
, and the speed of the ant at time  as
as 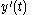 , we can write:
, we can write: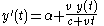
This is a first order linear differential equation, and it can be solved with standard methods. However, to do so requires some moderately advanced calculus. A much simpler approach considers the ant's position as a proportion of the distance from the starting-point to the target-point.
Consider coordinates
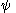 measured along the rope with the starting-point at
measured along the rope with the starting-point at 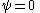 and the target-point at
and the target-point at 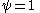 . In these coordinates, all points on the rope remain at a fixed position (in terms of
. In these coordinates, all points on the rope remain at a fixed position (in terms of 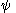 ) as the rope stretches. At time
) as the rope stretches. At time 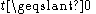 , a point at
, a point at 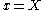 is at
is at 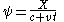 , and a speed
, and a speed 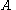 relative to the rope in terms of
relative to the rope in terms of 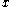 is equivalent to a speed
is equivalent to a speed  in terms of
in terms of  . So if we write the position of the ant in terms of
. So if we write the position of the ant in terms of 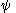 at time
at time  as
as 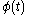 , and the speed of the ant in terms of
, and the speed of the ant in terms of 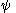 at time
at time  as
as 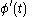 , we can write:
, we can write: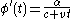
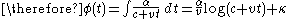 where
where 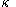 is a constant of integration.
is a constant of integration.Now,
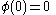 which gives
which gives 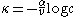 ,
,so
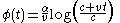 .
.If the ant reaches the target-point (which is at
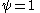 ) at time
) at time 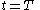 , we must have
, we must have 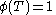 which gives us:
which gives us: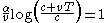
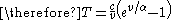
As this gives a finite value
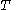 for all finite
for all finite  ,
, 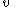 ,
, 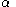 (
( ,
, 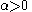 ), this means that, given sufficient time, the ant will complete the journey to the target-point. This formula can be used to find out how much time is required.
), this means that, given sufficient time, the ant will complete the journey to the target-point. This formula can be used to find out how much time is required.For the problem as originally stated,
 ,
, 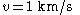 and
and 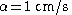 , which gives
, which gives 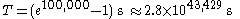 . This is a truly vast timespan, vast even in comparison to the estimated age of the universe, and the length of the rope after such a time is similarly huge, so it is only in a mathematical sense that the ant can ever reach the end of this particular rope.
. This is a truly vast timespan, vast even in comparison to the estimated age of the universe, and the length of the rope after such a time is similarly huge, so it is only in a mathematical sense that the ant can ever reach the end of this particular rope.Applications of the problem
This problem has a bearing on the question of whether light from distant galaxies can ever reach us if the universe is expanding. If the universe is expanding uniformly, this means that galaxies that are far enough away from us will have an apparent relative motion greater than the speed of light. This does not violate the relativistic constraint of not travelling faster than the speed of light, because the galaxy is not "travelling" as such—it is the space between us and the galaxy which is expanding and making new distance. The question is whether light leaving such a distant galaxy can ever reach us, given that the galaxy appears to be receding at a speed greater than the speed of light.By thinking of light photons as ants crawling along the rubber rope of space between the galaxy and us, it can be seen that just as the ant will eventually reach the end of the rope, given sufficient time, so the light from the distant galaxy will eventually reach earth, given sufficient time.

