
Appell series
Encyclopedia
In mathematics, Appell series
are a set of four hypergeometric series
F1, F2, F3, F4 of two variable
s that were introduced by and that generalize Gauss's hypergeometric series 2F1 of one variable. Appell established the set of partial differential equation
s of which these function
s are solutions, and found various reduction formulas and expressions of these series in terms of hypergeometric series of one variable.
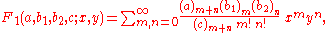
where the Pochhammer symbol
(q)n represents the rising factorial:
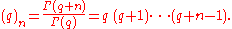
For other values of x and y the function F1 can be defined by analytic continuation
.
Similarly, the function F2 is defined for |x| + |y| < 1 by the series:

the function F3 for |x| < 1, |y| < 1 by the series:
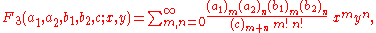
and the function F4 for |x|½ + |y|½ < 1 by the series:

s among contiguous functions. For example, a basic set of such relations for Appell's F1 is given by:




Any other relation valid for F1 can be derived from these four.
Similarly, all recurrence relations for Appell's F3 follow from this set of five:
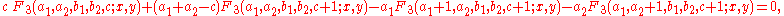


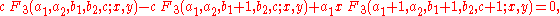
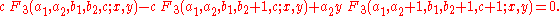
s result from the definition by a double series:
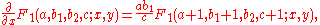
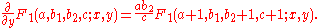
From its definition, Appell's F1 is further found to satisfy the following system of second-order differential equations
:
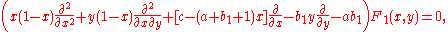
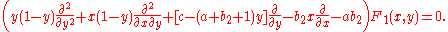
Similarly, for F3 the following derivatives result from the definition:

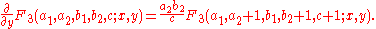
And for F3 the following system of differential equations is obtained:
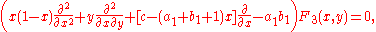
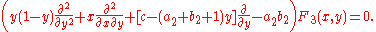
s involving elementary functions only. However, discovered that Appell's F1 can also be written as a one-dimensional Euler
-type integral
:
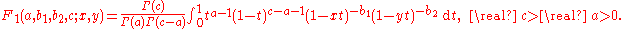
This representation can be verified by means of Taylor expansion
of the integrand, followed by termwise integration.
s F and E as well as the complete elliptic integral
Π are special cases of Appell's F1:
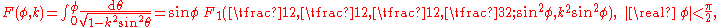
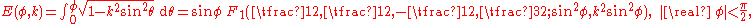
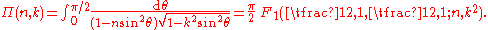
defined four functions similar to the Appell series, but depending on many variables rather than just the two variables x and y. These series were also studied by Appell. They satisfy certain partial differential equations, and can also be given in terms of Euler-type integrals and contour integral
s.
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
are a set of four hypergeometric series
Hypergeometric series
In mathematics, a generalized hypergeometric series is a series in which the ratio of successive coefficients indexed by n is a rational function of n. The series, if convergent, defines a generalized hypergeometric function, which may then be defined over a wider domain of the argument by...
F1, F2, F3, F4 of two variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
s that were introduced by and that generalize Gauss's hypergeometric series 2F1 of one variable. Appell established the set of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s of which these function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s are solutions, and found various reduction formulas and expressions of these series in terms of hypergeometric series of one variable.
Definitions
The Appell series F1 is defined for |x| < 1, |y| < 1 by the double series: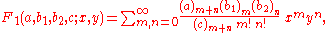
where the Pochhammer symbol
Pochhammer symbol
In mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
(q)n represents the rising factorial:
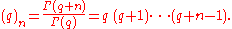
For other values of x and y the function F1 can be defined by analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
.
Similarly, the function F2 is defined for |x| + |y| < 1 by the series:

the function F3 for |x| < 1, |y| < 1 by the series:
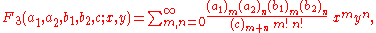
and the function F4 for |x|½ + |y|½ < 1 by the series:

Recurrence relations
Like the Gauss hypergeometric series 2F1, the Appell double series entail recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
s among contiguous functions. For example, a basic set of such relations for Appell's F1 is given by:




Any other relation valid for F1 can be derived from these four.
Similarly, all recurrence relations for Appell's F3 follow from this set of five:
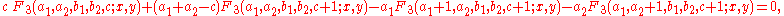


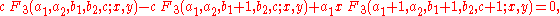
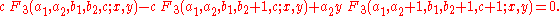
Derivatives and differential equations
For Appell's F1, the following derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s result from the definition by a double series:
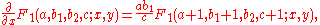
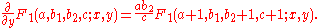
From its definition, Appell's F1 is further found to satisfy the following system of second-order differential equations
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
:
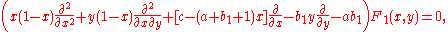
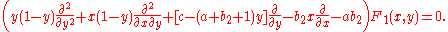
Similarly, for F3 the following derivatives result from the definition:

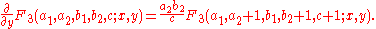
And for F3 the following system of differential equations is obtained:
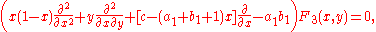
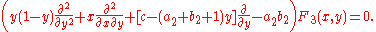
Integral representations
The four functions defined by Appell's double series can be represented in terms of double integralMultiple integral
The multiple integral is a type of definite integral extended to functions of more than one real variable, for example, ƒ or ƒ...
s involving elementary functions only. However, discovered that Appell's F1 can also be written as a one-dimensional Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
-type integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
:
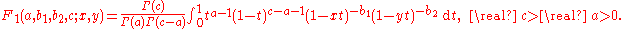
This representation can be verified by means of Taylor expansion
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of the integrand, followed by termwise integration.
Special cases
Picard's integral representation implies that the incomplete elliptic integralElliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
s F and E as well as the complete elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
Π are special cases of Appell's F1:
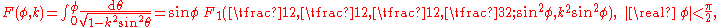
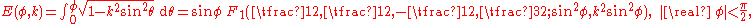
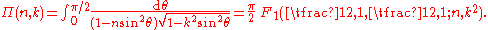
Related series
- There are seven related series of two variables, Φ1, Φ2, Φ3, Ψ1, Ψ2, Ξ1, and Ξ2, which generalize Kummer's confluent hypergeometric functionConfluent hypergeometric functionIn mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity...
1F1 of one variable and the confluent hypergeometric limit function 0F1 of one variable in a similar manner. The first of these was introduced by Pierre HumbertPierre Humbert (mathematician)Pierre Humbert was a French mathematician who worked on the theory of elliptic functions and introduced Humbert polynomials. He was the son of the mathematician Georges Humbert and married the daughter of Henri Andoyer.-References:...
in Humbert.
defined four functions similar to the Appell series, but depending on many variables rather than just the two variables x and y. These series were also studied by Appell. They satisfy certain partial differential equations, and can also be given in terms of Euler-type integrals and contour integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
s.

