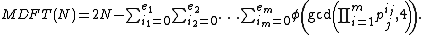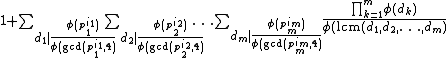Arithmetic complexity of the discrete Fourier transform
Encyclopedia
See Fast Fourier transform#Bounds on complexity and operation counts for a general summary of this issue.
(DFT) and hit upon remarkable results. Among them, a lower bound for the multiplicative (floating-point) complexity required to compute discrete transform
s, which is presented below. Let us denote by MDFT(N) the minimal multiplicative complexity for the exact computing a DFT of blocklength N [2].
Theorem (Heidman). For a given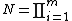 piei where pi, i = 1, ..., m are distinct primes and ei, i = 1, ..., m are positive integers, it follows then
piei where pi, i = 1, ..., m are distinct primes and ei, i = 1, ..., m are positive integers, it follows then
where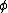 (.) is the Euler's totient function
(.) is the Euler's totient function
function, gcd(.,.) denotes the greatest common divisor
and lcm(.,.) is the least common multiple
.
Proof. See [1, page 98].
The application of this theorem for several values of N yields the complexities shown on the table. The difference between pointed complexities is striking. A further point to be observed is the fact that some people believe that fast Fourier transform
(FFT, Cooley–Tukey) is a close-to-optimum algorithm for computing a DFT. This minimal complexity is the same as that one required for the discrete Hartley transform
(DHT) of the same blocklength.
Recently, a new fast Fourier transform
algorithm was introduced [3,4], which is based on a multilayer Hadamard decomposition so as to evaluate a discrete Fourier transform
via a discrete Hartley transform
(DHT), which achieve the minimal floating-point multiplicative complexity for blocklengths until N = 24.
Bounds on the multiplicative complexity of FFT
In his PhD thesis in 1987 [1], Michael Heidman focused on the arithmetic theory of complexity for a discrete Fourier transformDiscrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(DFT) and hit upon remarkable results. Among them, a lower bound for the multiplicative (floating-point) complexity required to compute discrete transform
Discrete transform
In signal processing, discrete transforms are mathematical transforms, often linear transforms, of signals between discrete domains, such as between discrete time and discrete frequency....
s, which is presented below. Let us denote by MDFT(N) the minimal multiplicative complexity for the exact computing a DFT of blocklength N [2].
Theorem (Heidman). For a given
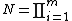 piei where pi, i = 1, ..., m are distinct primes and ei, i = 1, ..., m are positive integers, it follows then
piei where pi, i = 1, ..., m are distinct primes and ei, i = 1, ..., m are positive integers, it follows thenwhere
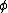 (.) is the Euler's totient function
(.) is the Euler's totient functionEuler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
function, gcd(.,.) denotes the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
and lcm(.,.) is the least common multiple
Least common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
.
Proof. See [1, page 98].
The application of this theorem for several values of N yields the complexities shown on the table. The difference between pointed complexities is striking. A further point to be observed is the fact that some people believe that fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT, Cooley–Tukey) is a close-to-optimum algorithm for computing a DFT. This minimal complexity is the same as that one required for the discrete Hartley transform
Discrete Hartley transform
A discrete Hartley transform is a Fourier-related transform of discrete, periodic data similar to the discrete Fourier transform , with analogous applications in signal processing and related fields. Its main distinction from the DFT is that it transforms real inputs to real outputs, with no...
(DHT) of the same blocklength.
-
- Table I – Minimal multiplicative complexity (expressed as the number of floating-point multiplications) required for computing a DFT for a few selected blocklengths.
N 2 3 4 5 6 8 12 16 24 32 48 64 128 256 definition 4 9 16 25 36 64 144 256 576 1024 2304 4096 16384 65536 FFT 2 * 8 * * 24 * 64 * 160 * 384 896 2048 MDFT(N) 0 1 0 4 2 2 4 10 12 32 38 84 198 438
- Table I – Minimal multiplicative complexity (expressed as the number of floating-point multiplications) required for computing a DFT for a few selected blocklengths.
Recently, a new fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
algorithm was introduced [3,4], which is based on a multilayer Hadamard decomposition so as to evaluate a discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
via a discrete Hartley transform
Discrete Hartley transform
A discrete Hartley transform is a Fourier-related transform of discrete, periodic data similar to the discrete Fourier transform , with analogous applications in signal processing and related fields. Its main distinction from the DFT is that it transforms real inputs to real outputs, with no...
(DHT), which achieve the minimal floating-point multiplicative complexity for blocklengths until N = 24.