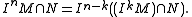Artin-Rees lemma
Encyclopedia
In mathematics
, the Artin–Rees lemma (also known as the Artin–Rees theorem) is a result in the theory of rings
and modules
. It was proved in the 1950s in independent works by the mathematician
s Emil Artin
and David Rees
; a special case was known to Oscar Zariski
prior to their work. The result is used to prove the exactness property of completion
.
in a Noetherian ring
R; let M be a finitely generated R-module and let N a submodule of M. Then there exists an integer
k ≥ 1 so that, for n ≥ k,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Artin–Rees lemma (also known as the Artin–Rees theorem) is a result in the theory of rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
and modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. It was proved in the 1950s in independent works by the mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
and David Rees
David Rees (mathematician)
David Rees ScD Cantab, FIMA, FRS is an emeritus professor of pure mathematics at the University of Exeter, having been head of the Mathematics / Mathematical Sciences Department at Exeter for many years....
; a special case was known to Oscar Zariski
Oscar Zariski
Oscar Zariski was a Russian mathematician and one of the most influential algebraic geometers of the 20th century.-Education:...
prior to their work. The result is used to prove the exactness property of completion
Completion (ring theory)
In abstract algebra, a completion is any of several related functors on rings and modules that result in complete topological rings and modules. Completion is similar to localization, and together they are among the most basic tools in analysing commutative rings. Complete commutative rings have...
.
Statement of the result
Let I be an idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
in a Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
R; let M be a finitely generated R-module and let N a submodule of M. Then there exists an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
k ≥ 1 so that, for n ≥ k,