Artin billiards
Encyclopedia
In mathematics
and physics
, the Artin billiard is a type of a dynamical billiard
first studied by Emil Artin
in 1924. It describes the geodesic motion of a free particle on the non-compact Riemann surface
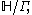where 
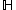is the upper half-plane endowed with the Poincaré metric
and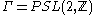
is the modular group
. It can be viewed as the motion on the fundamental domain
of the modular group with the sides identified.
The system is notable in that it is an exactly solvable system that is strongly chaotic
: it is not only ergodic, but is also strong mixing. As such, it is an example of an Anosov flow. Artin's paper used symbolic dynamics
for analysis of the system.
The quantum mechanical version of Artin's billiard is also exactly solvable. The eigenvalue spectrum consists of a bound state and a continuous spectrum above the energy
. The wave functions are given by Bessel function
s.
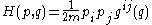
where m is the mass of the particle,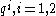
are the coordinates on the manifold, 
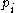are the conjugate momenta:
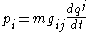
and
is the metric tensor
on the manifold. Because this is the free-particle Hamiltonian, the solution to the Hamilton-Jacobi equations of motion are simply given by the geodesic
s on the manifold.
In the case of the Artin billiards, the metric is given by the canonical Poincaré metric
on the upper half-plane. The non-compact Riemann surface
is a symmetric space
, and is defined as the quotient of the upper half-plane modulo the action of the elements of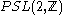
acting as Möbius transforms. The set
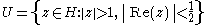
is a fundamental domain
for this action.
The manifold has, of course, one cusp
. This is the same manifold, when taken as the complex manifold
, that is the space on which elliptic curve
s and modular functions are studied.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Artin billiard is a type of a dynamical billiard
Dynamical billiards
A billiard is a dynamical system in which a particle alternates between motion in a straight line and specular reflections from a boundary. When the particle hits the boundary it reflects from it without loss of speed...
first studied by Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
in 1924. It describes the geodesic motion of a free particle on the non-compact Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
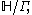where 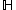is the upper half-plane endowed with the Poincaré metricPoincaré metric
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
and
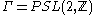is the modular groupModular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
. It can be viewed as the motion on the fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
of the modular group with the sides identified.
The system is notable in that it is an exactly solvable system that is strongly chaotic
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
: it is not only ergodic, but is also strong mixing. As such, it is an example of an Anosov flow. Artin's paper used symbolic dynamics
Symbolic dynamics
In mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics given by the shift operator...
for analysis of the system.
The quantum mechanical version of Artin's billiard is also exactly solvable. The eigenvalue spectrum consists of a bound state and a continuous spectrum above the energy
. The wave functions are given by Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s.
Exposition
The motion studied is that of a free particle sliding frictionlessly, namely, one having the HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
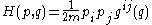
where m is the mass of the particle,
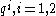are the coordinates on the manifold, 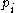are the conjugate momenta: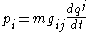and
is the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
on the manifold. Because this is the free-particle Hamiltonian, the solution to the Hamilton-Jacobi equations of motion are simply given by the geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s on the manifold.
In the case of the Artin billiards, the metric is given by the canonical Poincaré metric
on the upper half-plane. The non-compact Riemann surface
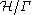is a symmetric spaceSymmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
, and is defined as the quotient of the upper half-plane modulo the action of the elements of
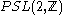acting as Möbius transforms. The set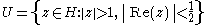is a fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
for this action.
The manifold has, of course, one cusp
Cusp neighborhood
In mathematics, a cusp neighborhood is defined as a set of points near a cusp.-Cusp neighborhood for a Riemann surface:The cusp neighborhood for a hyperbolic Riemann surface can be defined in terms of its Fuchsian model....
. This is the same manifold, when taken as the complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
, that is the space on which elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s and modular functions are studied.