In mathematics, an associahedron or Stasheff polytope K_n is a convex polytope

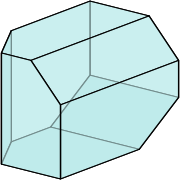
Convex polytope

A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...

 in which each vertex corresponds to a way of correctly inserting opening and closing parentheses in a word of n letters and the edges correspond to single application of the associativity

Associativity

In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...

 rule.

Initially Jim Stasheff considered these objects as curvilinear polytopes. K₄ is a pentagon

Pentagon

In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...

. K₅ is an enneahedron

Enneahedron

In geometry, a enneahedron is a polyhedron with 9 faces. There are 2606 topologically distinct enneahedra and none are regular, so this name is ambiguous.-Examples:...

, and its dual is the triaugmented triangular prism

Triaugmented triangular prism

In geometry, the triaugmented triangular prism is one of the Johnson solids . As the name suggests, it can be constructed by attaching square pyramids to each of the three equatorial faces of the triangular prism...

. The number of vertices in K_n + 1 is the nth Catalan number

Catalan number

In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...

.

See also

• Cyclohedron
  Cyclohedron
  In geometry, the cyclohedron or Bott–Taubes polytope is a certain -dimensional polytope that is useful in studying knot invariants....
  
  , a polytope whose definition allows parentheses to wrap around in cyclic order
• Permutohedron
  Permutohedron
  In mathematics, the permutohedron of order n is an -dimensional polytope embedded in an n-dimensional space, the vertices of which are formed by permuting the coordinates of the vector .-History:According to , permutohedra were first studied by...
  
  , a polytope defined from commutativity
  Commutativity
  In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
  
   in a similar way to the definition of the associahedron from associativity.
• Tamari lattice
  Tamari lattice
  In mathematics, a Tamari lattice, introduced by , is a partially ordered set in which the elements consist of different ways of grouping a sequence of objects into pairs using parentheses; for instance, for a sequence of four objects abcd, the five possible groupings are d, , d, a, and a...
  
  , a lattice
  Lattice (order)
  In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
  
   whose graph is the skeleton of the associahedron

External links

• Strange Associations - AMS column about Associahedra
• Ziegler's Lecture on the Associahedron. Notes from a lecture by Günter Ziegler at the Autonomous University of Barcelona
  Autonomous University of Barcelona
  The Autonomous University of Barcelona is a public university mostly located in Cerdanyola, near the city of Barcelona in Catalonia, Spain....
  
  , 2009.