
Assortativity
Encyclopedia
Assortativity is a preference for a network's nodes to attach to others that are similar or different in some way. Though the specific measure of similarity may vary, network theorists often examine assortativity in terms of a node's degree
. The addition of this characteristic to network models more closely approximates the behaviors of many real world networks.
Correlations between nodes of similar degree are often found in the mixing patterns
of many observable networks. For instance, in social networks, highly connected nodes tend to be connected with other high degree nodes. This tendency is referred to as assortative mixing
, or assortativity. On the other hand, technological and biological networks typically show disassortative mixing, or dissortativity, as high degree nodes tend to attach to low degree nodes.
 Assortativity is often operationalized as a correlation
Assortativity is often operationalized as a correlation
between two nodes. However, there are several ways to capture such a correlation. The two most prominent measures are the assortativity coefficient and the neighbor connectivity. These measures are outlined in more detail below.
The assortativity coefficient is given by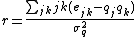 . The term
. The term 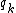 is the distribution of the remaining degree. This captures the number of edges leaving the node, other than the one that connects the pair. The distribution of this term is derived from the degree distribution
is the distribution of the remaining degree. This captures the number of edges leaving the node, other than the one that connects the pair. The distribution of this term is derived from the degree distribution 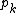 as
as 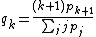 . Finally,
. Finally, 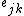 refers to the joint probability distribution of the remaining degrees of the two vertices. This quantity is symmetric on an undirected graph, and follows the sum rules
refers to the joint probability distribution of the remaining degrees of the two vertices. This quantity is symmetric on an undirected graph, and follows the sum rules  and
and  .
.
 Another means of capturing the degree correlation is by examining the properties of
Another means of capturing the degree correlation is by examining the properties of 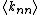 , or the average degree of neighbors of a node with degree k. This term is formally defined as:
, or the average degree of neighbors of a node with degree k. This term is formally defined as: 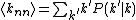 , where
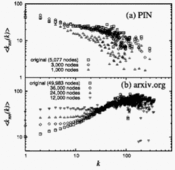
, where  is the conditional probability that an edge of node degree k points to a node with degree k. If this function is increasing, the network is assortative, since it shows that nodes of high degree connect, on average, to nodes of high degree. Alternatively, if the function is decreasing, the network is dissortative, since nodes of high degree tend to connect to nodes of lower degree. The function can be plotted on a graph (see Fig. 2) to depict the overall assortativity trend for a network.
is the conditional probability that an edge of node degree k points to a node with degree k. If this function is increasing, the network is assortative, since it shows that nodes of high degree connect, on average, to nodes of high degree. Alternatively, if the function is decreasing, the network is dissortative, since nodes of high degree tend to connect to nodes of lower degree. The function can be plotted on a graph (see Fig. 2) to depict the overall assortativity trend for a network.
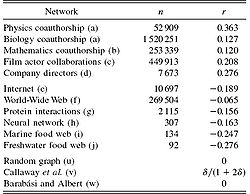 The assortative patterns of a variety of real world networks have been examined. For instance, Fig. 3 lists values of r for a variety of networks. Note that the social networks (the first five entries) have apparent assortative mixing. On the other hand, the technological and biological networks (the middle six entries) all appear to be disassortative. It has been suggested that this is because most networks have a tendency to evolve, unless otherwise constrained, towards their maximum entropy state—which is usually disassortative.
The assortative patterns of a variety of real world networks have been examined. For instance, Fig. 3 lists values of r for a variety of networks. Note that the social networks (the first five entries) have apparent assortative mixing. On the other hand, the technological and biological networks (the middle six entries) all appear to be disassortative. It has been suggested that this is because most networks have a tendency to evolve, unless otherwise constrained, towards their maximum entropy state—which is usually disassortative.
The table also has the value of r calculated analytically for two models of networks:
In the ER model, since edges are placed at random without regard to vertex degree, it follows that r = 0 in the limit of large graph size. Interestingly, the scale-free BA model also holds this property. For the BA model,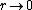 as
as 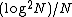 in the limit of large
in the limit of large 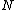 ..
..
Degree distribution
In the study of graphs and networks, the degree of a node in a network is the number of connections it has to other nodes and the degree distribution is the probability distribution of these degrees over the whole network.-Definition:...
. The addition of this characteristic to network models more closely approximates the behaviors of many real world networks.
Correlations between nodes of similar degree are often found in the mixing patterns
Mixing patterns
Mixing patterns refer to systematic tendencies of one type of nodes in a network to connect to another type. For instance, nodes might tend to link to others that are very similar or very different. This feature is common in many social networks, although it also appears sometimes in non-social...
of many observable networks. For instance, in social networks, highly connected nodes tend to be connected with other high degree nodes. This tendency is referred to as assortative mixing
Assortative mixing
In the study of complex networks, assortative mixing, or assortativity, is a bias in favor of connections between network nodes with similar characteristics. In the specific case of social networks, assortative mixing is also known as homophily...
, or assortativity. On the other hand, technological and biological networks typically show disassortative mixing, or dissortativity, as high degree nodes tend to attach to low degree nodes.
Measuring assortativity

Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
between two nodes. However, there are several ways to capture such a correlation. The two most prominent measures are the assortativity coefficient and the neighbor connectivity. These measures are outlined in more detail below.
Assortativity coefficient
The assortativity coefficient is essentially the Pearson correlation coefficient of degree between pairs of linked nodes. Hence, positive values of r indicate a correlation between nodes of similar degree, while negative values indicate relationships between nodes of different degree. In general, r lies between −1 and 1. When r = 1, the network is said to have perfect assortative mixing patterns, while at r = −1 the network is completely disassortative.The assortativity coefficient is given by
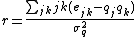 . The term
. The term 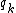 is the distribution of the remaining degree. This captures the number of edges leaving the node, other than the one that connects the pair. The distribution of this term is derived from the degree distribution
is the distribution of the remaining degree. This captures the number of edges leaving the node, other than the one that connects the pair. The distribution of this term is derived from the degree distribution 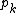 as
as 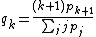 . Finally,
. Finally, 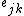 refers to the joint probability distribution of the remaining degrees of the two vertices. This quantity is symmetric on an undirected graph, and follows the sum rules
refers to the joint probability distribution of the remaining degrees of the two vertices. This quantity is symmetric on an undirected graph, and follows the sum rules  and
and  .
.Neighbor connectivity

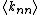 , or the average degree of neighbors of a node with degree k. This term is formally defined as:
, or the average degree of neighbors of a node with degree k. This term is formally defined as: 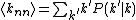 , where
, where  is the conditional probability that an edge of node degree k points to a node with degree k. If this function is increasing, the network is assortative, since it shows that nodes of high degree connect, on average, to nodes of high degree. Alternatively, if the function is decreasing, the network is dissortative, since nodes of high degree tend to connect to nodes of lower degree. The function can be plotted on a graph (see Fig. 2) to depict the overall assortativity trend for a network.
is the conditional probability that an edge of node degree k points to a node with degree k. If this function is increasing, the network is assortative, since it shows that nodes of high degree connect, on average, to nodes of high degree. Alternatively, if the function is decreasing, the network is dissortative, since nodes of high degree tend to connect to nodes of lower degree. The function can be plotted on a graph (see Fig. 2) to depict the overall assortativity trend for a network.Assortative mixing patterns of real networks

The table also has the value of r calculated analytically for two models of networks:
- the random graphRandom graphIn mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
of Erdos and Renyi - BA ModelBA modelThe Barabási–Albert model is an algorithm for generating random scale-free networks using a preferential attachment mechanism. Scale-free networks are widely observed in natural and man-made systems, including the Internet, the world wide web, citation networks, and some social...
(Barabási and Albert model)
In the ER model, since edges are placed at random without regard to vertex degree, it follows that r = 0 in the limit of large graph size. Interestingly, the scale-free BA model also holds this property. For the BA model,
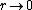 as
as 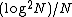 in the limit of large
in the limit of large 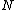 ..
..
