
Atkinson's theorem
Encyclopedia
In operator theory
, Atkinson's theorem (named for Frederick Valentine Atkinson) gives a characterization of Fredholm operator
s.
and L(H) the set of bounded operators on H. The following is the classical definition of a Fredholm operator
: an operator T ∈ L(H) is said to be a Fredholm operator if the kernel Ker(T) is finite dimensional, Ker(T*) is finite dimensional (where T* denotes the adjoint
of T), and the range
Ran(T) is closed.
Atkinson's theorem states:
In other words, an operator T ∈ L(H) is Fredholm, in the classical sense, if and only if its projection in the Calkin algebra
is invertible.
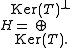
The restriction T : Ker(T)⊥ → Ran(T) is a bijection, and therefore invertible by the open mapping theorem
. Extend this inverse by 0 on Ran(T)⊥ = Ker(T*) to an operator S defined on all of H. Then I − TS is the finite-rank projection onto Ker(T*), and I − ST is the projection onto Ker(T). This proves the only if part of the theorem.
For the converse, suppose now that ST = I + C2 for some compact operator C2. If x ∈ Ker(T), then STx = x + C2x = 0. So Ker(T) is contained in an eigenspace of C2, which is finite dimensional (see spectral theory of compact operators
). Therefore Ker(T) is also finite dimensional. The same argument shows that Ker(T*) is also finite dimensional.
To prove that Ran(T) is closed, we make use of the approximation property
: let F be a finite-rank operator such that ||F − C2|| < r. Then for every x in Ker(F),
Thus T is bounded below on Ker(F), which implies that T(Ker(F)) is closed. On the other hand, T(Ker(F)⊥) is finite dimensional, since Ker(F)⊥ = Ran(F*) is finite dimensional. Therefore Ran(T) = T(Ker(F)) + T(Ker(F)⊥) is closed, and this proves the theorem.
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, Atkinson's theorem (named for Frederick Valentine Atkinson) gives a characterization of Fredholm operator
Fredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
s.
The theorem
Let H be a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and L(H) the set of bounded operators on H. The following is the classical definition of a Fredholm operator
Fredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
: an operator T ∈ L(H) is said to be a Fredholm operator if the kernel Ker(T) is finite dimensional, Ker(T*) is finite dimensional (where T* denotes the adjoint
Hermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
of T), and the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
Ran(T) is closed.
Atkinson's theorem states:
- A T ∈ L(H) is a Fredholm operator if and only if T is invertible modulo compact perturbation, i.e. TS = I + C1 and ST = I + C2 for some bounded operator S and compact operatorCompact operatorIn functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
s C1 and C2.
In other words, an operator T ∈ L(H) is Fredholm, in the classical sense, if and only if its projection in the Calkin algebra
Calkin algebra
In functional analysis, the Calkin algebra, named after John Wilson Calkin, is the quotient of B, the ring of bounded linear operators on a separable infinite-dimensional Hilbert space H, by the ideal K of compact operators....
is invertible.
Sketch of proof
The outline of a proof is as follows. For the ⇒ implication, express H as the orthogonal direct sum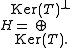
The restriction T : Ker(T)⊥ → Ran(T) is a bijection, and therefore invertible by the open mapping theorem
Open mapping theorem (functional analysis)
In functional analysis, the open mapping theorem, also known as the Banach–Schauder theorem , is a fundamental result which states that if a continuous linear operator between Banach spaces is surjective then it is an open map...
. Extend this inverse by 0 on Ran(T)⊥ = Ker(T*) to an operator S defined on all of H. Then I − TS is the finite-rank projection onto Ker(T*), and I − ST is the projection onto Ker(T). This proves the only if part of the theorem.
For the converse, suppose now that ST = I + C2 for some compact operator C2. If x ∈ Ker(T), then STx = x + C2x = 0. So Ker(T) is contained in an eigenspace of C2, which is finite dimensional (see spectral theory of compact operators
Spectral theory of compact operators
In functional analysis, compact operators are linear operators that map bounded sets to precompact sets. The set of compact operators acting on a Hilbert space H is the closure of the set of finite rank operators in the uniform operator topology. In general, operators on infinite dimensional spaces...
). Therefore Ker(T) is also finite dimensional. The same argument shows that Ker(T*) is also finite dimensional.
To prove that Ran(T) is closed, we make use of the approximation property
Approximation property
In mathematics, a Banach space is said to have the approximation property , if every compact operator is a limit of finite-rank operators. The converse is always true....
: let F be a finite-rank operator such that ||F − C2|| < r. Then for every x in Ker(F),
- ||S||·||Tx|| ≥ ||STx|| = ||x + C2x|| = ||x + Fx +C2x − Fx|| ≥ ||x|| − ||C2 − F||·||x|| ≥ (1 − r)||x||.
Thus T is bounded below on Ker(F), which implies that T(Ker(F)) is closed. On the other hand, T(Ker(F)⊥) is finite dimensional, since Ker(F)⊥ = Ran(F*) is finite dimensional. Therefore Ran(T) = T(Ker(F)) + T(Ker(F)⊥) is closed, and this proves the theorem.

