
Calkin algebra
Encyclopedia
In functional analysis
, the Calkin algebra, named after John Wilson Calkin, is the quotient
of B(H), the ring of bounded linear operators on a separable infinite-dimensional Hilbert space
H, by the ideal
K(H) of compact operator
s.
Since the compact operators is a (in fact, the only) maximal norm-closed ideal in B(H), the Calkin algebra is simple.
As a quotient of two C* algebras, the Calkin algebra is a C* algebra itself. There is a short exact sequence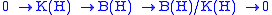
which induces a six-term cyclic exact sequence in K-theory
. Those operators in B(H) which are mapped to an invertible element of the Calkin algebra are called Fredholm operator
s, and their index
can be described both using K-theory and directly. One can conclude, for instance, that the collection of unitary operators in the Calkin algebra are homotopy classes indexed by the integers Z. This is in contrast to B(H), where the unitary operators are path connected.
As a C* algebra, the Calkin algebra is remarkable because it is not isomorphic to an algebra of operators on a separable Hilbert space; instead, a larger Hilbert space has to be chosen (the GNS theorem says that every C* algebra is isomorphic to an algebra of operators on a Hilbert space; for many other simple C* algebras, there are explicit descriptions of such Hilbert spaces, but for the Calkin algebra, this is not the case).
The same name is now used for the analogous construction for a Banach space
.
The Calkin algebra is the Corona algebra of the algebra of compact operators on a Hilbert space.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the Calkin algebra, named after John Wilson Calkin, is the quotient
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
of B(H), the ring of bounded linear operators on a separable infinite-dimensional Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H, by the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
K(H) of compact operator
Compact operator on Hilbert space
In functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
s.
Since the compact operators is a (in fact, the only) maximal norm-closed ideal in B(H), the Calkin algebra is simple.
As a quotient of two C* algebras, the Calkin algebra is a C* algebra itself. There is a short exact sequence
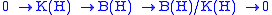
which induces a six-term cyclic exact sequence in K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
. Those operators in B(H) which are mapped to an invertible element of the Calkin algebra are called Fredholm operator
Fredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
s, and their index
Index
Index may refer to:-Business:* Index , a defunct UK catalogue retailer formerly owned by the Littlewoods group and known as Littlewoods Index* INDEX, a market research fair in Lucknow, India* Index fund, a collective investment scheme...
can be described both using K-theory and directly. One can conclude, for instance, that the collection of unitary operators in the Calkin algebra are homotopy classes indexed by the integers Z. This is in contrast to B(H), where the unitary operators are path connected.
As a C* algebra, the Calkin algebra is remarkable because it is not isomorphic to an algebra of operators on a separable Hilbert space; instead, a larger Hilbert space has to be chosen (the GNS theorem says that every C* algebra is isomorphic to an algebra of operators on a Hilbert space; for many other simple C* algebras, there are explicit descriptions of such Hilbert spaces, but for the Calkin algebra, this is not the case).
The same name is now used for the analogous construction for a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
.
The Calkin algebra is the Corona algebra of the algebra of compact operators on a Hilbert space.

