Auxiliary field
Encyclopedia
In physics
, and especially quantum field theory
, an auxiliary field
is one whose equations of motion admit a single solution. Therefore, the Lagrangian
describing such a field
contains an algebraic quadratic term and an arbitrary linear term, while it contains no kinetic terms (derivatives of the field):
.
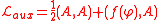The equation of motion for
is: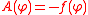 
and the Lagrangian becomes:
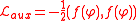. Auxiliary fields do not propagate and hence the content of any theory remains unchanged by adding such fields by hand.
If we have an initial Lagrangian
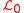describing a field 
then the Lagrangian describing both fields is:
.
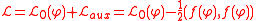Therefore, auxiliary fields can be employed to cancel quadratic terms in
in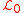 
and linearize the action
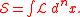
Examples of auxiliary fields are the complex scalar field F
in a chiral superfield
, the real scalar field D
in a vector superfield, the scalar field B in BRST and the field in the Hubbard-Stratonovich transformation
.
The quantum mechanical
effect of adding an auxiliary field is the same as the classical
, since the path integral
over such a field is Gaussian
. To wit: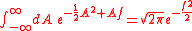
.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, and especially quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, an auxiliary field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
is one whose equations of motion admit a single solution. Therefore, the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
describing such a field
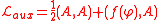contains an algebraic quadratic term and an arbitrary linear term, while it contains no kinetic terms (derivatives of the field):.The equation of motion for
is: 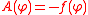and the Lagrangian becomes: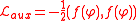. Auxiliary fields do not propagate and hence the content of any theory remains unchanged by adding such fields by hand.If we have an initial Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
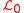describing a field then the Lagrangian describing both fields is: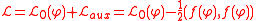.Therefore, auxiliary fields can be employed to cancel quadratic terms in
in 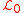and linearize the actionAction (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
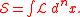
Examples of auxiliary fields are the complex scalar field F
F-term
In theoretical physics, one often analyzes theories with supersymmetry in which F-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates \theta^1,\theta^2,\bar\theta^1,\bar\theta^2,...
in a chiral superfield
Chiral superfield
In theoretical physics, one often analyzes theories with supersymmetry in which chiral superfields play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using the notion of superspace...
, the real scalar field D
D-term
In theoretical physics, one often analyzes theories with supersymmetry in which D-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates \theta^1,\theta^2,\bar\theta^1,\bar\theta^2,...
in a vector superfield, the scalar field B in BRST and the field in the Hubbard-Stratonovich transformation
Hubbard-Stratonovich transformation
The Hubbard–Stratonovich transformation is an exact mathematical transformation invented by Russian physicist Ruslan L. Stratonovich and popularized by British physicist John Hubbard...
.
The quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
effect of adding an auxiliary field is the same as the classical
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, since the path integral
Path integral
Path integral may refer to:* Line integral, the integral of a function along a curve* Functional integration, the integral of a functional over a space of curves...
over such a field is Gaussian
Gaussian integral
The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
. To wit:
.
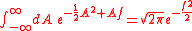