B-convex space
Encyclopedia
In functional analysis
, the class of B-convex spaces is a class of Banach space
. The concept of B-convexity was defined and used to characterize Banach spaces that have the strong law of large numbers by Anatole Beck in 1962; accordingly, "B-convexity" is understood as an abbreviation of Beck convexity. Beck proved the following theorem: A Banach space is B-convex if and only if
every sequence of independent
, symmetric, uniformly bounded and Radon random variables in that space satisfies the strong law of large numbers.
Let X be a Banach space with norm
|| ||. X is said to be B-convex if for some ε > 0 and some natural number
n, it holds true that whenever x1, ..., xn are elements of the closed unit ball of X, there is a choice of signs α1, ..., αn ∈ {−1, +1} such that
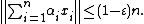
Later authors have shown that B-convexity is equivalent to a number of other important properties in the theory of Banach spaces. Being B-convex and having Rademacher type
were shown to be equivalent Banach-space properties by Gilles Pisier
.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the class of B-convex spaces is a class of Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. The concept of B-convexity was defined and used to characterize Banach spaces that have the strong law of large numbers by Anatole Beck in 1962; accordingly, "B-convexity" is understood as an abbreviation of Beck convexity. Beck proved the following theorem: A Banach space is B-convex if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
every sequence of independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, symmetric, uniformly bounded and Radon random variables in that space satisfies the strong law of large numbers.
Let X be a Banach space with norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
|| ||. X is said to be B-convex if for some ε > 0 and some natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n, it holds true that whenever x1, ..., xn are elements of the closed unit ball of X, there is a choice of signs α1, ..., αn ∈ {−1, +1} such that
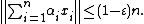
Later authors have shown that B-convexity is equivalent to a number of other important properties in the theory of Banach spaces. Being B-convex and having Rademacher type
were shown to be equivalent Banach-space properties by Gilles PisierGilles Pisier
Gilles I. Pisier is a Professor of Mathematics at the Pierre and Marie Curie University and a Distinguished Professor and A.G. and M.E. Owen Chair of Mathematics at the Texas A&M University. He is known for his contributions to several fields of mathematics, including functional analysis,...
.