Background independence
Encyclopedia
Background independence, also called universality, is the concept or assumption, fundamental to all physical sciences, that the nature of reality
is consistent throughout all of space
and time
. More specifically, no observer can, under any circumstances, perform a measurement that yields a result logically inconsistent with a previous measurement, under a set of rules that are independent of where and when the observations are made.
This is not a suggestion that spacetime
is uniform, merely that the fundamental rules governing the measurable characteristics of the physical universe
are the same everywhere, at all times.
using the principle in his Relativity
, the idea had been considered by a number of theorists, such as David Hume
, Charles Lyell
, and James Hutton
, under the name principle of universality. It postulates that the laws of nature discovered on Earth
apply throughout the universe.
There are several variations and corollaries:
(GR), as we will see below. More details and discussions can be found in Rovelli's book or the papers by Rovelli and Gaul and by Smolin.
It begins with an utterly trivial mathematical observation. Here is written the differential equation
for the simple harmonic oscillator
twice
except in Eq(1) the independent variable is x and in Eq(2) the independent variable is
. Once we find out that a solution to Eq(1) is 
, we immediately know that 
solves Eq(2). This observation combined with general covariance has profound implications for GR.
Assume pure gravity first. Say we have two coordinate system
s,
-coordinates and 
-coordinates. General covariance
demands the equations of motion have the same form in both coordinate systems, that is, we have exactly the same differential equation to solve in both coordinate systems, except in one the independent variable
is
and in the other it is 
. Once we find a metric function 
that solves the EOM in the 
-coordinates we immediately know (by exactly the same reasoning as above!) that the same function written as a function of 
solves the EOM in the 
-coordinates. As both metric functions have the same functional form but belong to different coordinate systems, they impose different spacetime geometries. Thus we have generated a second distinct solution!
Now comes the problem. Say the two coordinate systems coincide at first, but at some point after
we allow them to differ. We then have two solutions, they both have the same initial conditions yet they impose different spacetime geometries. The conclusion is that GR does not determine the proper time
between spacetime points! This argument (or rather a refinement of it) is known as Einstein's hole argument
. It is straightforward to include matter
- we have a larger set of differential equations but they still have the same form in all coordinates systems, so the same argument applies and again we obtain two solutions with the same initial conditions which impose different spacetime geometries. It is very important to note that we could not have generated these extra distinct solutions if spacetime were fixed and non-dynamic, and so the resolution to the hole argument, background independence, only comes about when we allow spacetime to be dynamic.
Before we can go on to understand this resolution we need to better understand these extra solutions. We can interpret these solutions as follows. For simplicity we first assume there is no matter. Define a metric function
whose value at 
is given by the value of 
at 
, i.e.
(see figure 1(a)). Now consider a coordinate system which assigns to
the same coordinate values that 
has in the x-coordinates (see figure 1(b)). We then have
Reality
In philosophy, reality is the state of things as they actually exist, rather than as they may appear or might be imagined. In a wider definition, reality includes everything that is and has been, whether or not it is observable or comprehensible...
is consistent throughout all of space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
and time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
. More specifically, no observer can, under any circumstances, perform a measurement that yields a result logically inconsistent with a previous measurement, under a set of rules that are independent of where and when the observations are made.
This is not a suggestion that spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
is uniform, merely that the fundamental rules governing the measurable characteristics of the physical universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
are the same everywhere, at all times.
Principle of universality
Prior to Albert EinsteinAlbert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
using the principle in his Relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the idea had been considered by a number of theorists, such as David Hume
David Hume
David Hume was a Scottish philosopher, historian, economist, and essayist, known especially for his philosophical empiricism and skepticism. He was one of the most important figures in the history of Western philosophy and the Scottish Enlightenment...
, Charles Lyell
Charles Lyell
Sir Charles Lyell, 1st Baronet, Kt FRS was a British lawyer and the foremost geologist of his day. He is best known as the author of Principles of Geology, which popularised James Hutton's concepts of uniformitarianism – the idea that the earth was shaped by slow-moving forces still in operation...
, and James Hutton
James Hutton
James Hutton was a Scottish physician, geologist, naturalist, chemical manufacturer and experimental agriculturalist. He is considered the father of modern geology...
, under the name principle of universality. It postulates that the laws of nature discovered on Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
apply throughout the universe.
There are several variations and corollaries:
- A stronger uniformity principle is that the laws of event causation have remained constant throughout time (uniformitarianismUniformitarianismIn the philosophy of naturalism, the uniformitarianism assumption is that the same natural laws and processes that operate in the universe now, have always operated in the universe in the past and apply everywhere in the universe. It has included the gradualistic concept that "the present is the...
) as well as applying everywhere in the 'modern' universe. - A corollaryCorollaryA corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
in physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
is the postulate that there has been no change in the fine-structure constant since the Big BangBig BangThe Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
. - Another corollary of the principle of uniformity states that everything that is now possible in principle was ever the case in the past.
Diffeomorphism invariance and background independence
The argument involves only the very basics of general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
(GR), as we will see below. More details and discussions can be found in Rovelli's book or the papers by Rovelli and Gaul and by Smolin.
It begins with an utterly trivial mathematical observation. Here is written the differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
for the simple harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
twice
- Eq(1)
- Eq(2)
except in Eq(1) the independent variable is x and in Eq(2) the independent variable is
. Once we find out that a solution to Eq(1) is , we immediately know that solves Eq(2). This observation combined with general covariance has profound implications for GR.Assume pure gravity first. Say we have two coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
s,
-coordinates and -coordinates. General covarianceGeneral covariance
In theoretical physics, general covariance is the invariance of the form of physical laws under arbitrary differentiable coordinate transformations...
demands the equations of motion have the same form in both coordinate systems, that is, we have exactly the same differential equation to solve in both coordinate systems, except in one the independent variable
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
is
and in the other it is . Once we find a metric function that solves the EOM in the -coordinates we immediately know (by exactly the same reasoning as above!) that the same function written as a function of solves the EOM in the -coordinates. As both metric functions have the same functional form but belong to different coordinate systems, they impose different spacetime geometries. Thus we have generated a second distinct solution!Now comes the problem. Say the two coordinate systems coincide at first, but at some point after
we allow them to differ. We then have two solutions, they both have the same initial conditions yet they impose different spacetime geometries. The conclusion is that GR does not determine the proper timeProper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
between spacetime points! This argument (or rather a refinement of it) is known as Einstein's hole argument
Hole argument
In general relativity, the hole argument is a "paradox" which much troubled Albert Einstein while developing his famous field equation.It is incorrectly interpreted by some philosophers as an argument against manifold substantialism, a doctrine that the manifold of events in spacetime are a...
. It is straightforward to include matter
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
- we have a larger set of differential equations but they still have the same form in all coordinates systems, so the same argument applies and again we obtain two solutions with the same initial conditions which impose different spacetime geometries. It is very important to note that we could not have generated these extra distinct solutions if spacetime were fixed and non-dynamic, and so the resolution to the hole argument, background independence, only comes about when we allow spacetime to be dynamic.
Before we can go on to understand this resolution we need to better understand these extra solutions. We can interpret these solutions as follows. For simplicity we first assume there is no matter. Define a metric function
whose value at is given by the value of at , i.e.
- Eq(3)
.
(see figure 1(a)). Now consider a coordinate system which assigns to
the same coordinate values that has in the x-coordinates (see figure 1(b)). We then have
- Eq(4)
where
are the coordinate values of 
in the x-coordinate system.
When we allow the coordinate values to range over all permissible values, Eq(4) is precisely the condition that the two metric functions have the same functional form! We see that the new solution is generated by dragging the original metric function over the spacetime manifold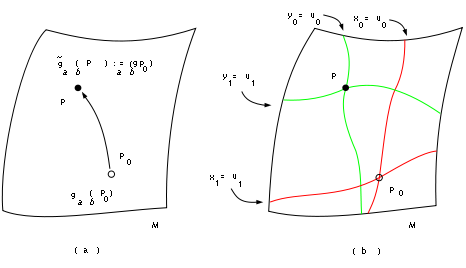
ManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
while keeping the coordinate lines "attached", see Fig 1. It is important to realise that we are not performing a coordinate transformation here, this is what's known as an active diffeomorphism (coordinate transformations are called passive diffeomorphisms). It should be easy to see that when we have matter present, simultaneously performing an active diffeomorphism on the gravitational and matter fields generates the new distinct solution.
The resolution to the hole argument (mainly taken from Rovelli's book) is as follows. As GR does not determine the distance between spacetime points, how the gravitational and matter fields are located over spacetime, and so the values they take at spacetime points, can have no physical meaning. What GR does determine, however, are the mutual relations that exist between the gravitational field and the matter fields (i.e. the value the gravitational field takes where the matter field takes such and such value). From these mutual relations we can form a notion of matter being located with respect to the gravitational field and vice-versa, (see Rovelli's for exposition). What Einstein discovered was that physical entities are located with respect to one another only, independent of the spacetime manifold. This independence is background independence.
Since the hole argument is a direct consequence of the general covariance of GR, this led Einstein to state:
"That this requirement of general covariance, which takes away from space and time the last remnant of physical objectivity, is a natural one, ..."
The term "active diffeomorphism" has been used, instead of just "diffeomorphism", to emphasize that this is not a case of simple coordinate transformations. It is active diffeomorphisms which are the gauge transformations of GR and they should not be confused with the freedom of choosing coordinates on the space-time M. Invariance under coordinate transformations is not a special feature of GR as all physical theories are invariant under coordinate transformations. (Indeed, the mathematical definition of a diffeomorphism is a transformation which relates manifolds with equivalent topological and differentiable structure, but not necessarily equivalent metrics. For example, a diffeomorphism can turn a doughnutDoughnutA doughnut or donut is a fried dough food and is popular in many countries and prepared in various forms as a sweet snack that can be homemade or purchased in bakeries, supermarkets, food stalls, and franchised specialty outlets...
into a tea cup.)
Whether or not Lorentz invariance is broken in the low-energy limit of loop quantum gravityLoop quantum gravityLoop quantum gravity , also known as loop gravity and quantum geometry, is a proposed quantum theory of spacetime which attempts to reconcile the theories of quantum mechanics and general relativity...
(LQG), the theory is formally background independent. The equations of LQG are not embedded in, or presuppose, space and time, except for its invariant topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. Instead, they are expected to give rise to space and time at distances which are large compared to the Planck length. At present, it remains unproven that LQG's description of spacetime at the Planck scale has the right continuum limit, described by general relativity with possible quantum corrections.
Manifest background-independence
This is primarily an aesthetic rather than a physical requirement. It is analogous to requiring in differential geometryGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
that equations be written in a form that is independent of the choice of charts and coordinate embeddings. If a background-independent formalism is present, it can lead to simpler and more elegant equations. However there is no physical content in requiring that a theory be manifestly background-independent - for example, the equations of general relativity can be rewritten in local coordinates without affecting the physical implications.
String theory
Although the physics of string theoryString theoryString theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
can in principle be background-independent, perturbative formulations of this theory do not make this independence manifest because they require starting with a particular solution and performing a perturbative expansion about this background. Non-perturbative formulations such as matrix theoryMatrix string theoryIn physics, Matrix string theory is a set of equations that describe superstring theory in a non-perturbative framework. Type IIA string theory can be shown to be equivalent to a maximally supersymmetric two-dimensional gauge theory, the gauge group of which is U for a large value of N...
and AdS/CFTAdS/CFT correspondenceIn physics, the AdS/CFT correspondence , sometimes called the Maldacena duality, is the conjectured equivalence between a string theory and gravity defined on one space, and a quantum field theory without gravity defined on the conformal boundary of this space, whose dimension is lower by one or more...
resolve that issue and are fully background independent.
String field theory
The classical background-independent approach to string theory is string field theoryString field theoryString field theory is a formalism in string theory in which the dynamics of relativistic strings is reformulated in the language of quantum field theory...
. Although string field theory has been useful to understand tachyon condensationTachyon condensationIn particle physics, theoretical processes that eliminate or resolve particles or fields into better understood phenomena are called, by extension and metaphor with the macroscopic process, "condensation"...
, most string theorists believe that it will never be useful to understand non-perturbative physics of string theory.
Loop quantum gravity
A very different approach to quantum gravity called loop quantum gravityLoop quantum gravityLoop quantum gravity , also known as loop gravity and quantum geometry, is a proposed quantum theory of spacetime which attempts to reconcile the theories of quantum mechanics and general relativity...
is background-independent by design. It dispenses with the concept of a background spacetime metric and instead deals with discrete structures called spin foamSpin foamIn physics, a spin foam is a topological structure made out of two-dimensional faces that represents one of the configurations that must be summed to obtain a Feynman's path integral description of quantum gravity...
s. The crucial point is that spin foams don't live in spacetime - they are spacetime. Therefore, high-level properties of spacetime, such as dimensionality and topology, are emergent long-distance features of the corresponding spin foam.
One of the major shortcomings of loop quantum gravity is that, as of 2009, it has not been shown that the theory in fact reduces to Einstein's general relativity in the continuumContinuumContinuum may refer to:* Continuum , anything that goes through a gradual transition from one condition, to a different condition, without any abrupt changes-Linguistics:...
limit. Since GR equations were used initially to construct the theory, many researchers assume that they can be recovered, but this has neither been explicitly proved nor disproved. In addition, incorporating matter into the theory is an ongoing problem.
History of background independent theories
This dichotomy between background dependent and independent theories is sometimes traced back as far as the antagonism between NewtonIsaac NewtonSir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and LeibnizGottfried LeibnizGottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
about absolute vs. relational spaceRelational spaceThe relational theory of space is a metaphysical theory according to which space is composed of relations between objects, with the implication that it cannot exist in the absence of matter. Its opposite is the container theory...
. Most physicists would claim that the choice of approach is merely philosophical so far as no different falsifiableFalsifiabilityFalsifiability or refutability of an assertion, hypothesis or theory is the logical possibility that it can be contradicted by an observation or the outcome of a physical experiment...
claims follow, not unlike the question of interpretations of quantum mechanics. However, two philosophers of sciencePhilosophy of scienceThe philosophy of science is concerned with the assumptions, foundations, methods and implications of science. It is also concerned with the use and merit of science and sometimes overlaps metaphysics and epistemology by exploring whether scientific results are actually a study of truth...
, Imre LakatosImre LakatosImre Lakatos was a Hungarian philosopher of mathematics and science, known for his thesis of the fallibility of mathematics and its 'methodology of proofs and refutations' in its pre-axiomatic stages of development, and also for introducing the concept of the 'research programme' in his...
and Elie Zahar, have argued that research programResearch programA research program is a coordinated set of projects undertaking related research, often at national or even international level, with government funding....
s can be driven by metaphysicalMetaphysicsMetaphysics is a branch of philosophy concerned with explaining the fundamental nature of being and the world, although the term is not easily defined. Traditionally, metaphysics attempts to answer two basic questions in the broadest possible terms:...
questions and so adopting the view of background independence may lead to different results.
See also
- Causal dynamical triangulation
- Loop quantum gravityLoop quantum gravityLoop quantum gravity , also known as loop gravity and quantum geometry, is a proposed quantum theory of spacetime which attempts to reconcile the theories of quantum mechanics and general relativity...
- Quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
- Cosmological principleCosmological PrincipleIn modern physical cosmology, the cosmological principle is the working assumption that observers on Earth do not occupy an unusual or privileged location within the universe as a whole, judged as observers of the physical phenomena produced by uniform and universal laws of physics...
External links