
Baker's theorem
Encyclopedia
In transcendence theory
, a mathematical discipline, Baker's theorem gives a lower bound for linear combinations of logarithm
s of algebraic number
s. The result, proved by , subsumed many earlier results in transcendental number theory and solved a problem posed by Alexander Gelfond
nearly fifteen years earlier.
Baker used this to prove the transcendence of many numbers, and to derive effective bounds for the solutions of some Diophantine equations, and to solve the problem of finding all imaginary quadratic field
s with class number
1.
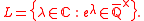
Using this notation several results in transcendental number theory become much easier to state, for example the Hermite–Lindemann theorem becomes the statement that any nonzero element of L is transcendental.
In 1934, Alexander Gelfond and Theodor Schneider
independently proved the Gelfond–Schneider theorem
. This result is usually stated as: if a is algebraic and not equal to 0 or 1, and if b is algebraic and irrational, then ab is transcendental. Equivalently, though, it says that if λ1 and λ2 are elements of L that are linearly independent over the rational numbers, then they are linearly independent over the algebraic numbers. So if λ1 and λ2 are elements of L and λ2 isn't zero, then the quotient λ1/λ2 is either a rational number or transcendental. It can't be an algebraic irrational number like √2.
Although proving this result of "rational linear independence implies algebraic linear independence" for two elements of L was sufficient for his and Schneider's result, Gelfond felt that it was crucial to extend this result to arbitrarily many elements of L. Indeed, from :
This problem was solved fourteen years later by Alan Baker and has since had numerous applications not only to transcendence theory but in algebraic number theory
and the study of Diophantine equations as well. Baker received the Fields medal
in 1970 for both this work and his applications of it to Diophantine equations.
where H is the maximum of the heights of the β's and C is an effectively computable
number depending on n, the λ's, and the maximum d of the degrees of the β's. (If β0 is nonzero then the assumption that the λ's are linearly independent can be dropped.) In particular this number is nonzero, so 1 and the λ's are linearly independent over the algebraic numbers.
Just as the Gelfond–Schneider theorem is equivalent to the statement about the transcendence of numbers of the form ab, so too Baker's theorem implies the transcendence of numbers of the form
where the bi are all algebraic, irrational, and 1, b1,…,bn are linearly independent over the rationals, and the ai are all algebraic and not 0 or 1.
also gave several versions with explicit constants. For example,
if eλj=αj has height at most Aj≥4 and all the numbers βj have height at most B≥4 then the linear form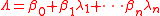
is either 0 or satisfies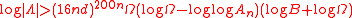
where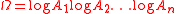
and the field generated by all the α's and β's over the rationals has degree at most d. In the special case when β0=0 and all the βj are rational integers, the rightmost term log Ω can be deleted.
The main ideas of the proof are illustrated by the proof of the following qualitative version of the theorem of described by : if the numbers 2πi and log a1,..., log an are linearly independent over the rational numbers, for nonzero algebraic numbers a1,..., an, then they are linearly independent over the algebraic numbers. The precise quantitative version of Bakers theory can be proved by replacing the conditions that things are zero by conditions that things are sufficiently small throughout the proof.
The main idea of Bakers proof is to construct an auxiliary function
Φ(z1,...,zn−1) of several variables that vanishes to high order at many points of the form Φ(l,l,...,l), then repeatedly show that it vanishes to lower order at even more points of this form. Finally the fact that it vanishes (to order 1) at enough points of this form implies using Vandermonde determinants that there is a multiplicative relation between the numbers ai.

for algebraic numbers α1,...,αn, β1,...,βn−1
The function Φ is of the form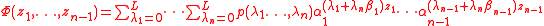
The integer coefficients p are chosen so that they are not all zero and Φ and its derivatives of order at most some constant M vanish at z1=...=zn−1 = l, for integers l with 0≤l≤h for some constant h. This is possible because these conditions are homogeneous linear equations in the coefficients p, which have a non-zero solution provided the number of unknown variables p is larger than the number of equations. The linear relation between the logs of the α's is needed to cut down the number of linear equations that have to be satisfied. Moreover, using Siegel's lemma
, the sizes of the coefficients p can be chosen to be not too large. The constants L, h, and M have to be carefully adjusted to that the next part of the proof works, and are subject to some constraints, which are roughly:
The constraints can be satisfied by taking h to be sufficiently large, M to be some fixed power of h, and L to be a slightly smaller power of h. Baker took M to be about h2 and L to be about h2−1/2n.
The linear relation between the logarithms of the α's is used to reduce L slightly; roughly speaking, without it the condition Ln must be larger than about Mn−1h would become Ln must be larger than about Mnh, which is incompatible with the condition that L is somewhat smaller than M.
One then takes J large enough that h1+J/8n > (L+1)n (J larger than about 16n will do if h2 > L) so that that Φ(l,...l)=0 for all integers l with 1≤ l≤ (L+1)n.
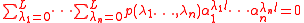
This consists of (L+1)n homogeneous linear equations in the (L+1)n unknowns p, and by assumption has a non-zero solution p, so the determinant of the matrix of coefficients must vanish. However this matrix is a Vandermonde matrix, so the formula for the determinant of such a matrix forces an equality two of the values
so the numbers α1,...,αn are multiplicatively dependent. Taking logs then shows that 2πi, log α1,...,log αn are linearly dependent over the rationals.
showed how to eliminate the assumption about 2πi in the theorem. This requires a modification of the final step of the proof. One shows that many derivatives of the function φ(z)=Φ(z,...z) vanish at z=0, by an argument similar to the one above. But these equations for the first (L+1)n derivatives again give a homogeneous set of linear equations for the coefficients p, so the determinant is zero, and is again a Vandermonde determinant, this time for the numbers λ1log α1+...λnlog αn. So two of these expressions must be the same which shows that log α1,...,log αn are linearly dependent over the rationals.
gave an inhomogeneous version of the theorem, showing that
β0+β1logα1 + ... +βnlogαn is nonzero for nonzero algebraic numbers β0, ..., βn, α1,..., αn, and moreover giving an effective lower bound for it. The proof is similar to the homogeneous case: one can assume that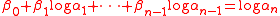
and one inserts an extra variable z0 into Φ as follows: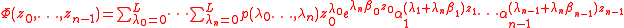
, and does not imply the six exponentials theorem
nor, clearly, the still open four exponentials conjecture
.
The main reason Gelfond desired an extension of his result was not just for a slew of new transcendental numbers. In 1935 he used the tools he had developed to prove the Gelfond–Schneider theorem
to derive a lower bound for the quantity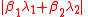
where β1 and β2 are algebraic and λ1 and λ2 are in L. Baker's proof gave lower bounds for quantities like the above but with arbitrarily many terms, and he could use these bounds to develop effective means of tackling Diophantine equations and to solve Gauss' class number problem.
. So far no progress has been made on this problem at all. It has been conjectured that if λ1,…,λn are elements of L that are linearly independent over the rational numbers, then they are algebraically independent too. This is a special case of Schanuel's conjecture, but so far it remains to be proved that there even exist two algebraic numbers whose logarithms are algebraically independent. Indeed, Baker's theorem rules out linear relations between logarithms of algebraic numbers unless there are trivial reasons for them; the next most simple case, that of ruling out homogeneous
quadratic relations, is the still open four exponentials conjecture
.
Similarly, extending the result to algebraic independence but in the p-adic setting, and using the p-adic logarithm function
, remains an open problem. It is known that proving algebraic independence of linearly independent p-adic logarithms of algebraic p-adic numbers would prove Leopoldt's conjecture
on the p-adic ranks of units of a number field.
Transcendence theory
Transcendence theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.-Transcendence:...
, a mathematical discipline, Baker's theorem gives a lower bound for linear combinations of logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s of algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s. The result, proved by , subsumed many earlier results in transcendental number theory and solved a problem posed by Alexander Gelfond
Alexander Gelfond
Alexander Osipovich Gelfond was a Soviet mathematician, author of Gelfond's theorem.-Biography:Alexander Gelfond was born in St Petersburg, Russian Empire in the family of a professional physician and amateur philosopher Osip Isaakovich Gelfond. He entered the Moscow State University in 1924,...
nearly fifteen years earlier.
Baker used this to prove the transcendence of many numbers, and to derive effective bounds for the solutions of some Diophantine equations, and to solve the problem of finding all imaginary quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
s with class number
Class number
In mathematics, class number may refer to* Class number , the number of conjugacy classes of a group*The size of the ideal class group of a number ring*The number of equivalence classes of binary quadratic forms of a given discriminant...
1.
History
To simplify notation we introduce the set L of logarithms of nonzero algebraic numbers, that is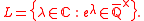
Using this notation several results in transcendental number theory become much easier to state, for example the Hermite–Lindemann theorem becomes the statement that any nonzero element of L is transcendental.
In 1934, Alexander Gelfond and Theodor Schneider
Theodor Schneider
Theodor Schneider was a German mathematician, best known for providing proof of what is now known as the Gelfond–Schneider theorem in 1935....
independently proved the Gelfond–Schneider theorem
Gelfond–Schneider theorem
In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider...
. This result is usually stated as: if a is algebraic and not equal to 0 or 1, and if b is algebraic and irrational, then ab is transcendental. Equivalently, though, it says that if λ1 and λ2 are elements of L that are linearly independent over the rational numbers, then they are linearly independent over the algebraic numbers. So if λ1 and λ2 are elements of L and λ2 isn't zero, then the quotient λ1/λ2 is either a rational number or transcendental. It can't be an algebraic irrational number like √2.
Although proving this result of "rational linear independence implies algebraic linear independence" for two elements of L was sufficient for his and Schneider's result, Gelfond felt that it was crucial to extend this result to arbitrarily many elements of L. Indeed, from :
This problem was solved fourteen years later by Alan Baker and has since had numerous applications not only to transcendence theory but in algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
and the study of Diophantine equations as well. Baker received the Fields medal
Fields Medal
The Fields Medal, officially known as International Medal for Outstanding Discoveries in Mathematics, is a prize awarded to two, three, or four mathematicians not over 40 years of age at each International Congress of the International Mathematical Union , a meeting that takes place every four...
in 1970 for both this work and his applications of it to Diophantine equations.
Statement
With the above notation, Baker's theorem is a nonhomogeneous generalisation of the Gelfond–Schneider theorem. Specifically it states:- If λ1,…,λn are elements of L that are linearly independent over the rational numbers, then for any algebraic numbers β0,…,βn, not all zero, we have

where H is the maximum of the heights of the β's and C is an effectively computable
Effective results in number theory
For historical reasons and in order to have application to the solution of Diophantine equations, results in number theory have been scrutinised more than in other branches of mathematics to see if their content is effectively computable...
number depending on n, the λ's, and the maximum d of the degrees of the β's. (If β0 is nonzero then the assumption that the λ's are linearly independent can be dropped.) In particular this number is nonzero, so 1 and the λ's are linearly independent over the algebraic numbers.
Just as the Gelfond–Schneider theorem is equivalent to the statement about the transcendence of numbers of the form ab, so too Baker's theorem implies the transcendence of numbers of the form

where the bi are all algebraic, irrational, and 1, b1,…,bn are linearly independent over the rationals, and the ai are all algebraic and not 0 or 1.
also gave several versions with explicit constants. For example,
if eλj=αj has height at most Aj≥4 and all the numbers βj have height at most B≥4 then the linear form
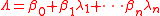
is either 0 or satisfies
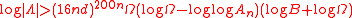
where
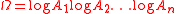
and the field generated by all the α's and β's over the rationals has degree at most d. In the special case when β0=0 and all the βj are rational integers, the rightmost term log Ω can be deleted.
Baker's method
Baker's proof of his theorem is an extension of the argument given by .The main ideas of the proof are illustrated by the proof of the following qualitative version of the theorem of described by : if the numbers 2πi and log a1,..., log an are linearly independent over the rational numbers, for nonzero algebraic numbers a1,..., an, then they are linearly independent over the algebraic numbers. The precise quantitative version of Bakers theory can be proved by replacing the conditions that things are zero by conditions that things are sufficiently small throughout the proof.
The main idea of Bakers proof is to construct an auxiliary function
Auxiliary function
In mathematics, auxiliary functions are an important construction in transcendental number theory. They are functions that appear in most proofs in this area of mathematics and that have specific, desirable properties, such as taking the value zero for many arguments, or having a zero of high...
Φ(z1,...,zn−1) of several variables that vanishes to high order at many points of the form Φ(l,l,...,l), then repeatedly show that it vanishes to lower order at even more points of this form. Finally the fact that it vanishes (to order 1) at enough points of this form implies using Vandermonde determinants that there is a multiplicative relation between the numbers ai.
Construction of the function Φ
Assume there is a relation
for algebraic numbers α1,...,αn, β1,...,βn−1
The function Φ is of the form
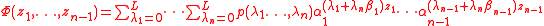
The integer coefficients p are chosen so that they are not all zero and Φ and its derivatives of order at most some constant M vanish at z1=...=zn−1 = l, for integers l with 0≤l≤h for some constant h. This is possible because these conditions are homogeneous linear equations in the coefficients p, which have a non-zero solution provided the number of unknown variables p is larger than the number of equations. The linear relation between the logs of the α's is needed to cut down the number of linear equations that have to be satisfied. Moreover, using Siegel's lemma
Siegel's lemma
In transcendental number theory and Diophantine approximation, Siegel's lemma refers to bounds on the solutions of linear equations obtained by the construction of auxiliary functions. The existence of these polynomials was proven by Axel Thue; Thue's proof used Dirichlet's box principle. Carl...
, the sizes of the coefficients p can be chosen to be not too large. The constants L, h, and M have to be carefully adjusted to that the next part of the proof works, and are subject to some constraints, which are roughly:
- L must be somewhat smaller than M to make the argument about extra zeros below work.
- A small power of h must be larger than L to make the final step of the proof work.
- Ln must be larger than about Mn−1h in order that it is possible to solve for the coefficients p.
The constraints can be satisfied by taking h to be sufficiently large, M to be some fixed power of h, and L to be a slightly smaller power of h. Baker took M to be about h2 and L to be about h2−1/2n.
The linear relation between the logarithms of the α's is used to reduce L slightly; roughly speaking, without it the condition Ln must be larger than about Mn−1h would become Ln must be larger than about Mnh, which is incompatible with the condition that L is somewhat smaller than M.
Zeros of Φ(l,l,...l)
The next step is to show that Φ vanishes to slightly smaller order at many more points of the form z1 = ...zn−1 =l for integers l. This idea was Baker's key innovation: previous work on this problem involved trying to increase the number of derivatives that vanish while keeping the number of points fixed, which does not seem to work in the multivariable case. This is done by combining two ideas; First one shows that the derivatives at these points are quite small, by using the fact that many derivatives of Φ vanish at many nearby points. Then one shows that derivatives of Φ at this point are given by algebraic integers times known constants. If an algebraic integer has all its conjugates bounded by a known constant, then it cannot be too small unless it is zero, because the product of all conjugates of a nonzero algebraic integer is at least 1 in absolute value. Combining these two ideas implies that Φ vanishes to slightly smaller order at many more points z1 = ...zn−1 =l. This part of the argument requires that Φ does not increase too rapidly; the growth of Φ depends on the size of L, so requires a bound on the size of L, which turns out to be roughly that L must be somewhat smaller than M. More precisely, Baker showed that since Φ vanishes to order M at h consecutive integers, it also vanishes to order M/2 at h1+1/8n consecutive integers 1, 2, 3,.... Repeating this argument J times shows that Φ vanishes to order M/2J at h1+J/8n points, provided that h is sufficiently large and L is somewhat smaller than M/2J.One then takes J large enough that h1+J/8n > (L+1)n (J larger than about 16n will do if h2 > L) so that that Φ(l,...l)=0 for all integers l with 1≤ l≤ (L+1)n.
Completion of the proof
The condition that Φ(l,...l)=0 for all integers l with 1≤ l≤ (L+1)n can be written as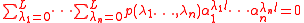
This consists of (L+1)n homogeneous linear equations in the (L+1)n unknowns p, and by assumption has a non-zero solution p, so the determinant of the matrix of coefficients must vanish. However this matrix is a Vandermonde matrix, so the formula for the determinant of such a matrix forces an equality two of the values

so the numbers α1,...,αn are multiplicatively dependent. Taking logs then shows that 2πi, log α1,...,log αn are linearly dependent over the rationals.
Extensions and generalizations
in fact gave a quantitative version of the theorem, giving effective lower bounds for the linear form in logarithms. This is done by a similar argument, except statements about something being zero are replaced by statements giving a small upper bound for it, and so on.showed how to eliminate the assumption about 2πi in the theorem. This requires a modification of the final step of the proof. One shows that many derivatives of the function φ(z)=Φ(z,...z) vanish at z=0, by an argument similar to the one above. But these equations for the first (L+1)n derivatives again give a homogeneous set of linear equations for the coefficients p, so the determinant is zero, and is again a Vandermonde determinant, this time for the numbers λ1log α1+...λnlog αn. So two of these expressions must be the same which shows that log α1,...,log αn are linearly dependent over the rationals.
gave an inhomogeneous version of the theorem, showing that
β0+β1logα1 + ... +βnlogαn is nonzero for nonzero algebraic numbers β0, ..., βn, α1,..., αn, and moreover giving an effective lower bound for it. The proof is similar to the homogeneous case: one can assume that
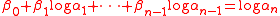
and one inserts an extra variable z0 into Φ as follows:
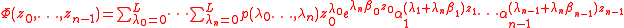
Corollaries
As mentioned above, the theorem includes numerous earlier transcendence results concerning the exponential function, such as the Hermite–Lindemann theorem and Gelfond–Schneider theorem. It is not quite as encompassing as the still unproven Schanuel's conjectureSchanuel's conjecture
In mathematics, specifically transcendence theory, Schanuel's conjecture is a conjecture made by Stephen Schanuel in the 1960s concerning the transcendence degree of certain field extensions of the rational numbers.-Statement:The conjecture is as follows:...
, and does not imply the six exponentials theorem
Six exponentials theorem
In mathematics, specifically transcendental number theory, the six exponentials theorem is a result that, given the right conditions on the exponents, guarantees the transcendence of at least one of a set of exponentials.-Statement:...
nor, clearly, the still open four exponentials conjecture
Four exponentials conjecture
In mathematics, specifically the field of transcendental number theory, the four exponentials conjecture is a conjecture which, given the right conditions on the exponents, would guarantee the transcendence of at least one of four exponentials...
.
The main reason Gelfond desired an extension of his result was not just for a slew of new transcendental numbers. In 1935 he used the tools he had developed to prove the Gelfond–Schneider theorem
Gelfond–Schneider theorem
In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider...
to derive a lower bound for the quantity
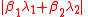
where β1 and β2 are algebraic and λ1 and λ2 are in L. Baker's proof gave lower bounds for quantities like the above but with arbitrarily many terms, and he could use these bounds to develop effective means of tackling Diophantine equations and to solve Gauss' class number problem.
Extensions
Baker's theorem grants us the linear independence over the algebraic numbers of logarithms of algebraic numbers. This is weaker than proving their algebraic independenceAlgebraic independence
In abstract algebra, a subset S of a field L is algebraically independent over a subfield K if the elements of S do not satisfy any non-trivial polynomial equation with coefficients in K...
. So far no progress has been made on this problem at all. It has been conjectured that if λ1,…,λn are elements of L that are linearly independent over the rational numbers, then they are algebraically independent too. This is a special case of Schanuel's conjecture, but so far it remains to be proved that there even exist two algebraic numbers whose logarithms are algebraically independent. Indeed, Baker's theorem rules out linear relations between logarithms of algebraic numbers unless there are trivial reasons for them; the next most simple case, that of ruling out homogeneous
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
quadratic relations, is the still open four exponentials conjecture
Four exponentials conjecture
In mathematics, specifically the field of transcendental number theory, the four exponentials conjecture is a conjecture which, given the right conditions on the exponents, would guarantee the transcendence of at least one of four exponentials...
.
Similarly, extending the result to algebraic independence but in the p-adic setting, and using the p-adic logarithm function
P-adic exponential function
In mathematics, particularly p-adic analysis, the p-adic exponential function is a p-adic analogue of the usual exponential function on the complex numbers...
, remains an open problem. It is known that proving algebraic independence of linearly independent p-adic logarithms of algebraic p-adic numbers would prove Leopoldt's conjecture
Leopoldt's conjecture
In algebraic number theory, Leopoldt's conjecture, introduced by , states that p-adic regulator of a number field does not vanish. The p-adic regulator is an analogue of the usual...
on the p-adic ranks of units of a number field.

