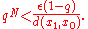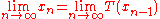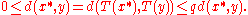Banach fixed point theorem
Encyclopedia
In mathematics, the Banach fixed-point theorem
(also known as the contraction mapping theorem or contraction mapping principle) is an important tool in the theory of metric space
s; it guarantees the existence and uniqueness of fixed points
of certain self-maps of metric spaces, and provides a constructive method to find those fixed points. The theorem is named after Stefan Banach
(1892–1945), and was first stated by him in 1922.
on X, i.e.: there is a nonnegative real number
q < 1 such that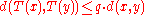
for all x, y in X. Then the map T admits one and only one fixed-point x* in X (this means T(x*) = x*). Furthermore, this fixed point can be found as follows: start with an arbitrary element x0 in X and define an iterative
sequence by xn = T(xn−1) for n = 1, 2, 3, ... This sequence converges
, and its limit is x*. The following inequality describes the speed of convergence
:
Equivalently,
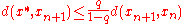
and
Any such value of q is called a Lipschitz constant for T, and the smallest one is sometimes called "the best Lipschitz constant" of T.
Note that the requirement d(T(x), T(y)) < d(x, y) for all unequal x and y is in general not enough to ensure the existence of a fixed point, as is shown by the map T :[1,∞) → [1,∞) with T(x) = x + 1/x, which lacks a fixed point. However, if the metric space X is compact
, then this weaker assumption does imply the existence and uniqueness of a fixed point, that can be easily found as a minimizer of d(x, T(x)) : indeed, a minimizer exists by compactness, and has to be a fixed point of T. It then easily follows that the fixed point is the limit of any sequence of iterations of T.
When using the theorem in practice, the most difficult part is typically to define X properly so that T actually maps elements from X to X, i.e. that T(x) is always an element of X.
. For each 
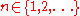, define 
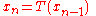. We claim that for all 
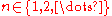, the following is true:
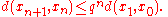
To show this, we will proceed using induction. The above statement is true for the case
, for
Suppose the above statement holds for some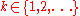
. Then we have
Fixed-point theorem
In mathematics, a fixed-point theorem is a result saying that a function F will have at least one fixed point , under some conditions on F that can be stated in general terms...
(also known as the contraction mapping theorem or contraction mapping principle) is an important tool in the theory of metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s; it guarantees the existence and uniqueness of fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of certain self-maps of metric spaces, and provides a constructive method to find those fixed points. The theorem is named after Stefan Banach
Stefan Banach
Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
(1892–1945), and was first stated by him in 1922.
The theorem
Let (X, d) be a non-empty complete metric space. Let T : X → X be a contraction mappingContraction mapping
In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...
on X, i.e.: there is a nonnegative real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
q < 1 such that
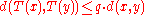
for all x, y in X. Then the map T admits one and only one fixed-point x* in X (this means T(x*) = x*). Furthermore, this fixed point can be found as follows: start with an arbitrary element x0 in X and define an iterative
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
sequence by xn = T(xn−1) for n = 1, 2, 3, ... This sequence converges
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
, and its limit is x*. The following inequality describes the speed of convergence
Rate of convergence
In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
:
Equivalently,
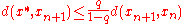
and
Any such value of q is called a Lipschitz constant for T, and the smallest one is sometimes called "the best Lipschitz constant" of T.
Note that the requirement d(T(x), T(y)) < d(x, y) for all unequal x and y is in general not enough to ensure the existence of a fixed point, as is shown by the map T :
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, then this weaker assumption does imply the existence and uniqueness of a fixed point, that can be easily found as a minimizer of d(x, T(x)) : indeed, a minimizer exists by compactness, and has to be a fixed point of T. It then easily follows that the fixed point is the limit of any sequence of iterations of T.
When using the theorem in practice, the most difficult part is typically to define X properly so that T actually maps elements from X to X, i.e. that T(x) is always an element of X.
Proof
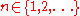Choose any. For each , define 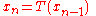. We claim that for all 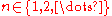, the following is true: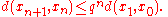To show this, we will proceed using induction. The above statement is true for the case
, forSuppose the above statement holds for some
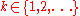. Then we have-
The inductive assumption is used going from line three to line four. By the principle of mathematical induction, for all
, the above claim is true.
Let
. Since 
, we can find a large 
so that
Using the claim above, we have that for any
, 
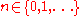with 
,
-
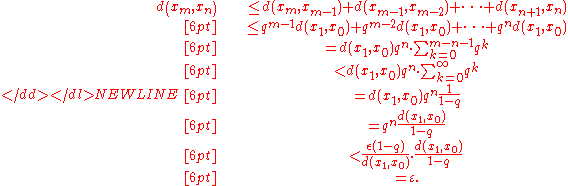
The inequality in line one follows from repeated applications of the triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
; the series in line four is a geometric series with
and hence it converges. The above shows that 
is a Cauchy sequenceCauchy sequenceIn mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
in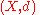
and hence convergent by completeness. So let 
. We make two claims: (1) 
is a fixed pointFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of
. That is, 
; (2)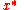 
is the only fixed point of 
in 
.
To see (1), we take the limit of both sides of the recurrence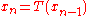
,
Since T is a contraction mapping, it is continuous, so we may take the limit inside:
. Thus, 
.
To show (2), we suppose that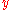
also satisfies 
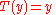. Then
Remembering that
, the above implies that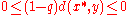 
, which shows that 
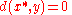, whence by positive definitenessDefinite bilinear formIn mathematics, a definite bilinear form is a bilinear form B over some vector space V such that the associated quadratic formQ=B \,...
,
and the proof is complete.
Applications
- A standard application is the proof of the Picard–Lindelöf theoremPicard–Lindelöf theoremIn mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
about the existence and uniqueness of solutions to certain ordinary differential equationOrdinary differential equationIn mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s. The sought solution of the differential equation is expressed as a fixed point of a suitable integral operator which transforms continuous functions into continuous functions. The Banach fixed-point theorem is then used to show that this integral operator has a unique fixed point.
- One consequence of the Banach fixed-point theorem is that small Lipschitz perturbation of the identity are bi-lipschitz homeomorphisms. Let
be an open set of a Banach space 
; let 
denote the identity (inclusion) map and let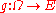 
be a Lipschitz map of constant k<1. Then (i) 
is an open subset of 
:precisely, for any 
such that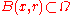 
one has
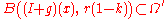; (ii)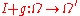 
is a bi-lipschitz homeomorphism; precisely,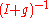
is still of the form
,
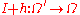with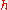
a Lipschitz map of constant 
A direct consequence of this result yields the proof of the inverse function theoremInverse function theoremIn mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
.
Converses
Several converses of the Banach contraction principle exist. The following is due to Czesław Bessaga, from 1959:
Let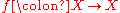
be a map of an abstract set such that each iterateIterated functionIn mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
ƒn has a unique fixed point. Let q be a real number, 0 < q < 1. Then there exists a complete metric on X such that ƒ is contractive, and q is the contraction constant.
Generalizations
There are a number of generalizations as immediate corollaries , which are of some interest for the sake of applications. Let
be a map on a complete non-empty metric space.
- Assume that some iterate
of T is a contraction. Then T has a unique fixed point. - Assume that for all
and 
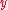in 
, 
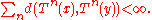Then T has a unique fixed point.
However, in most applications the existence and unicity of a fixed point can be shown directly with the standard Banach fixed point theorem, by a suitable choice of the metric that makes the map T a contraction. Indeed, the above result by Bessaga strongly suggests to look for such a metric. See also the article on fixed point theorems in infinite-dimensional spacesFixed point theorems in infinite-dimensional spacesIn mathematics, a number of fixed-point theorems in infinite-dimensional spaces generalise the Brouwer fixed-point theorem. They have applications, for example, to the proof of existence theorems for partial differential equations....
for generalizations. -
-
