Contraction mapping
Encyclopedia
In mathematics
, a contraction mapping, or contraction, on a metric space
(M,d) is a function
f from M to itself, with the property that there is some nonnegative real number
such that for all x and y in M,
The smallest such value of k is called the Lipschitz constant of f. Contractive maps are sometimes called Lipschitzian maps. If the above condition is instead satisfied for
k ≤ 1, then the mapping is said to be a non-expansive map.
More generally, the idea of a contractive mapping can be defined for maps between metric spaces. Thus, if (M,d) and (N,d) are two metric spaces, and
, then there is a constant k such that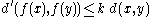
for all x and y in M.
Every contraction mapping is Lipschitz continuous and hence uniformly continuous (for a Lipschitz continuous function, the constant k is no longer necessarily less than 1).
A contraction mapping has at most one fixed point
. Moreover, the Banach fixed point theorem
states that every contraction mapping on a nonempty complete metric space has a unique fixed point, and that for any x in M the iterated function
sequence x, f (x), f (f (x)), f (f (f (x))), ... converges to the fixed point. This concept is very useful for iterated function systems where contraction mappings are often used. Banach's fixed point theorem is also applied in proving the existence of solutions of ordinary differential equations, and is used in one proof of the inverse function theorem
.
can be strengthened to a firmly non-expansive mapping in a Hilbert space
H if the following holds for all x and y in H:
where
This is a special case of
averaged nonexpansive operators with 
. A firmly non-expansive mapping is always non-expansive, via the Cauchy–Schwarz inequality
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a contraction mapping, or contraction, on a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
(M,d) is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f from M to itself, with the property that there is some nonnegative real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
such that for all x and y in M,The smallest such value of k is called the Lipschitz constant of f. Contractive maps are sometimes called Lipschitzian maps. If the above condition is instead satisfied for
k ≤ 1, then the mapping is said to be a non-expansive map.
More generally, the idea of a contractive mapping can be defined for maps between metric spaces. Thus, if (M,d) and (N,d) are two metric spaces, and
, then there is a constant k such that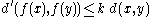for all x and y in M.
Every contraction mapping is Lipschitz continuous and hence uniformly continuous (for a Lipschitz continuous function, the constant k is no longer necessarily less than 1).
A contraction mapping has at most one fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
. Moreover, the Banach fixed point theorem
Banach fixed point theorem
In mathematics, the Banach fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points...
states that every contraction mapping on a nonempty complete metric space has a unique fixed point, and that for any x in M the iterated function
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
sequence x, f (x), f (f (x)), f (f (f (x))), ... converges to the fixed point. This concept is very useful for iterated function systems where contraction mappings are often used. Banach's fixed point theorem is also applied in proving the existence of solutions of ordinary differential equations, and is used in one proof of the inverse function theorem
Inverse function theorem
In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
.
Firmly non-expansive mapping
A non-expansive mapping with can be strengthened to a firmly non-expansive mapping in a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H if the following holds for all x and y in H:
where
This is a special case of
averaged nonexpansive operators with . A firmly non-expansive mapping is always non-expansive, via the Cauchy–Schwarz inequalityCauchy–Schwarz inequality
In mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
.