Behnke–Stein theorem
Encyclopedia
In mathematics, especially several complex variables
, the Behnke–Stein theorem states that a union of an increasing sequence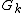
(i.e., 
) of domains of holomorphy
is again a domain of holomorphy.
This is related to the fact that an increasing union of pseudoconvex domains is pseudoconvex and so it can be proven using that fact and the solution of the Levi problem. Though historically this theorem was in fact used to solve the Levi problem.
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, the Behnke–Stein theorem states that a union of an increasing sequence
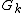(i.e., ) of domains of holomorphyDomain of holomorphy
In mathematics, in the theory of functions of several complex variables, a domain of holomorphy is a set which is maximal in the sense that there exists a holomorphic function on this set which cannot be extended to a bigger set....
is again a domain of holomorphy.
This is related to the fact that an increasing union of pseudoconvex domains is pseudoconvex and so it can be proven using that fact and the solution of the Levi problem. Though historically this theorem was in fact used to solve the Levi problem.