
Benford's law
Encyclopedia

Data
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
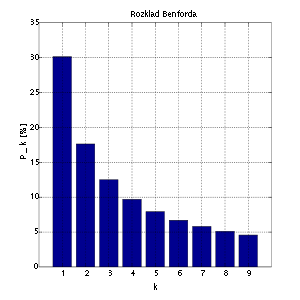
, the leading digit is distributed in a specific, non-uniform way. According to this law, the first digit is about 30% of the time, and larger digits occur as the leading digit with lower and lower frequency, to the point where 9 as a first digit occurs less than 5% of the time. This distribution of first digits is the same as the widths of gridlines on the logarithmic scale
Logarithmic scale
A logarithmic scale is a scale of measurement using the logarithm of a physical quantity instead of the quantity itself.A simple example is a chart whose vertical axis increments are labeled 1, 10, 100, 1000, instead of 1, 2, 3, 4...
.
This counter-intuitive result has been found to apply to a wide variety of data sets, including electricity bills, street addresses, stock prices, population numbers, death rates, lengths of rivers, physical
Physical constant
A physical constant is a physical quantity that is generally believed to be both universal in nature and constant in time. It can be contrasted with a mathematical constant, which is a fixed numerical value but does not directly involve any physical measurement.There are many physical constants in...
and mathematical constant
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
s, and processes described by power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
s (which are very common in nature). It tends to be most accurate when values are distributed across multiple orders of magnitude
Order of magnitude
An order of magnitude is the class of scale or magnitude of any amount, where each class contains values of a fixed ratio to the class preceding it. In its most common usage, the amount being scaled is 10 and the scale is the exponent being applied to this amount...
.
The graph to the right shows Benford's law for base 10
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
. There is a generalization of the law to numbers expressed in other bases (for example, base 16
Hexadecimal
In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...
), and also a generalization to second digits and later digits.
It is named after physicist Frank Benford
Frank Benford
Frank Albert Benford, Jr., was an American electrical engineer and physicist best known for rediscovering and generalizing Benford's Law, a statistical statement about the occurrence of digits in lists of data.Benford is also known for having devised, in 1937, an instrument for measuring the...
, who stated it in 1938,
although it had been previously stated by Simon Newcomb
Simon Newcomb
Simon Newcomb was a Canadian-American astronomer and mathematician. Though he had little conventional schooling, he made important contributions to timekeeping as well as writing on economics and statistics and authoring a science fiction novel.-Early life:Simon Newcomb was born in the town of...
in 1881.
Mathematical statement
A set of numbers is said to satisfy Benford's law if the leading digit d (d ∈ {1, …, 9}) occurs with probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
Numerically, the leading digits have the following distribution in Benford's law, where d is the leading digit and P(d) the probability:
| d | P(d) | Relative size of P(d) |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 |
The quantity P(d) is proportional to the space between d and d + 1 on a logarithmic scale
Logarithmic scale
A logarithmic scale is a scale of measurement using the logarithm of a physical quantity instead of the quantity itself.A simple example is a chart whose vertical axis increments are labeled 1, 10, 100, 1000, instead of 1, 2, 3, 4...
. Therefore, this is the distribution expected if the logarithms of the numbers (but not the numbers themselves) are uniformly and randomly distributed
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
. For example, a one-digit number x starts with the digit 1 if 1 ≤ x < 2, and starts with the digit 9 if 9 ≤ x < 10. Therefore, x starts with the digit 1 if log 1 ≤ log x < log 2, or starts with 9 if log 9 ≤ log x < log 10. The interval [log 1, log 2] is much wider than the interval [log 9, log 10] (0.30 and 0.05 respectively); therefore if log x is uniformly and randomly distributed, it is much more likely to fall into the wider interval than the narrower interval, i.e. more likely to start with 1 than with 9. The probabilities are proportional to the interval widths, and this gives the equation above. (The above discussion assumed x is a one-digit number, but the result is the same no matter how many digits x has.)
An extension of Benford's law predicts the distribution of first digits in other bases
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
besides decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
; in fact, any base b ≥ 2. The general form is:
For b = 2 (the binary number system
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
), Benford's law is true but trivial: All binary numbers (except for 0) start with the digit 1. (On the other hand, the generalization of Benford's law to second and later digits is not trivial, even for binary numbers.) Also, Benford's law does not apply to unary systems
Unary numeral system
The unary numeral system is the bijective base-1 numeral system. It is the simplest numeral system to represent natural numbers: in order to represent a number N, an arbitrarily chosen symbol representing 1 is repeated N times. For example, using the symbol | , the number 6 is represented as ||||||...
such as tally marks
Tally marks
Tally marks, or hash marks, are a unary numeral system. They are a form of numeral used for counting. They allow updating written intermediate results without erasing or discarding anything written down...
.
Benford's "law" is different from a typical mathematical theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
: It is an empirical statement about real-world datasets. It applies to some datasets but not all, and even when it applies it is at best only approximate, never exact.
Example
Examining a list of the heights of the 60 tallest structures in the world by category shows that 1 is by far the most common leading digit, irrespective of the unit of measurement:| Leading digit | meters | feet | In Benford's law | ||
|---|---|---|---|---|---|
| Count | % | Count | % | ||
| 1 | 26 | 43.3% | 18 | 30.0% | 30.1% |
| 2 | 7 | 11.7% | 8 | 13.3% | 17.6% |
| 3 | 9 | 15.0% | 8 | 13.3% | 12.5% |
| 4 | 6 | 10.0% | 6 | 10.0% | 9.7% |
| 5 | 4 | 6.7% | 10 | 16.7% | 7.9% |
| 6 | 1 | 1.7% | 5 | 8.3% | 6.7% |
| 7 | 2 | 3.3% | 2 | 3.3% | 5.8% |
| 8 | 5 | 8.3% | 1 | 1.7% | 5.1% |
| 9 | 0 | 0.0% | 2 | 3.3% | 4.6% |
History
The discovery of this fact goes back to 1881, when the American astronomer Simon NewcombSimon Newcomb
Simon Newcomb was a Canadian-American astronomer and mathematician. Though he had little conventional schooling, he made important contributions to timekeeping as well as writing on economics and statistics and authoring a science fiction novel.-Early life:Simon Newcomb was born in the town of...
noticed that in logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
tables (used at that time to perform calculations), the earlier pages (which contained numbers that started with 1) were much more worn than the other pages. Newcomb's published result is the first known instance of this observation and includes a distribution on the second digit, as well. Newcomb proposed a law that the probability of a single number N being the first digit of a number was equal to log(N + 1) − log(N).
The phenomenon was rediscovered in 1938 by the physicist Frank Benford
Frank Benford
Frank Albert Benford, Jr., was an American electrical engineer and physicist best known for rediscovering and generalizing Benford's Law, a statistical statement about the occurrence of digits in lists of data.Benford is also known for having devised, in 1937, an instrument for measuring the...
, who checked it on a wide variety of data sets and was credited for it. In 1995, Ted Hill proved the result about mixed distributions mentioned below. The discovery was named after Benford making it an example of Stigler's law.
Outcomes of exponential growth processes
The precise form of Benford's law can be explained if one assumes that the logarithms of the numbers are uniformly distributed; for instance that a number is just as likely to be between 100 and 1000 (logarithm between 2 and 3) as it is between 10,000 and 100,000 (logarithm between 4 and 5). For many sets of numbers, especially sets that grow exponentiallyExponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
such as incomes and stock prices, this is a reasonable assumption.
For example, if a quantity increases continuously and doubles every year, then it will be twice its original value after one year, four times its original value after two years, eight times its original value after three years, and so on. When this quantity reaches a value of 100, the value will have a leading digit of 1 for a year, reaching 200 at the end of the year. Over the course of the next year, the value increases from 200 to 400; it will have a leading digit of 2 for a little over seven months, and 3 for the remaining five months. In the third year, the leading digit will pass through 4, 5, 6, and 7, spending less and less time with each succeeding digit, reaching 800 at the end of the year. Early in the fourth year, the leading digit will pass through 8 and 9. The leading digit returns to 1 when the value reaches 1000, and the process starts again, taking a year to double from 1000 to 2000.
From this example, it can be seen that if the value is sampled at uniformly distributed random times throughout those years, it is more likely to be measured when the leading digit is 1, and successively less likely to be measured with higher leading digits.
This example makes it plausible that data tables that involve measurements of exponentially growing quantities will agree with Benford's Law. But the law also appears to hold for many cases where an exponential growth pattern is not obvious.
Scale invariance

Yard
A yard is a unit of length in several different systems including English units, Imperial units and United States customary units. It is equal to 3 feet or 36 inches...
s (multiplication by a constant), for example, the distribution must be unchanged — it is scale invariant, and the only continuous distribution that fits this is one whose logarithm is uniformly distributed.
For example, the first (non-zero) digit of the length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
s or distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
s of objects should have the same distribution whether the unit of measurement is feet, yards, or anything else. But there are three feet in a yard, so the probability that the first digit of a length in yards is 1 must be the same as the probability that the first digit of a length in feet is 3, 4, or 5. Applying this to all possible measurement scales gives a logarithmic distribution, and combined with the fact that log10(1) = 0 and log10(10) = 1 gives Benford's law. That is, if there is a distribution of first digits, it must apply to a set of data regardless of what measuring units are used, and the only distribution of first digits that fits that is the Benford Law.
Multiple probability distributions
For numbers drawn from certain distributions, for example IQ scores, human heights or other variables following normal distributions, the law is not valid. However, if one "mixes" numbers from those distributions, for example by taking numbers from newspaper articles, Benford's law reappears. This can also be proven mathematically: if one repeatedly "randomly" chooses a probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
(from an uncorrelated set) and then randomly chooses a number according to that distribution, the resulting list of numbers will obey Benford's law. Élise Janvresse and Thierry de la Rue from CNRS advanced as similar probabilistic explanation for the appearance of Benford's law in everyday-life numbers, by showing that it arises naturally when one considers mixtures of uniform distributions.
Applications
In 1972, Hal VarianHal Varian
Hal Ronald Varian is an economist specializing in microeconomics and information economics. He is the Chief Economist at Google and he holds the title of emeritus professor at the University of California, Berkeley where he was founding dean of the School of Information...
suggested that the law could be used to detect possible fraud in lists of socio-economic data submitted in support of public planning decisions. Based on the plausible assumption that people who make up figures tend to distribute their digits fairly uniformly, a simple comparison of first-digit frequency distribution from the data with the expected distribution according to Benford's law ought to show up any anomalous results. Following this idea, Mark Nigrini showed that Benford's law could be used in forensic accounting
Forensic accounting
Forensic accounting is the specialty practice area of accountancy that describes engagements that result from actual or anticipated disputes or litigation. "Forensic" means "suitable for use in a court of law", and it is to that standard and potential outcome that forensic accountants generally...
and audit
Audit
The general definition of an audit is an evaluation of a person, organization, system, process, enterprise, project or product. The term most commonly refers to audits in accounting, but similar concepts also exist in project management, quality management, and energy conservation.- Accounting...
ing as an indicator of accounting and expenses fraud.
In the United States, evidence based on Benford's law is legally admissible in criminal cases at the federal, state, and local levels.
Benford's law has been invoked as evidence of fraud in the 2009 Iranian elections
Iranian presidential election, 2009
Iran's tenth presidential election was held on 12 June 2009, with incumbent Mahmoud Ahmadinejad running against three challengers. The next morning the Islamic Republic News Agency, Iran's official news agency, announced that with two-thirds of the votes counted, Ahmadinejad had won the election...
. However, other experts consider Benford's law essentially useless as a statistical indicator of election fraud in general.
Limitations
Benford's law can only be applied to data that are distributed across multiple orders of magnitude. For instance, one might expect that Benford's law would apply to a list of numbers representing the populations of UK villages beginning with 'A', or representing the values of small insurance claims. But if a "village" is a settlement with population between 300 and 999, or a "small insurance claim" is a claim between $50 and $100, then Benford's law will not apply.Consider the probability distributions shown below, plotted on a log scale.
In each case, the total area in red is the relative probability that the first digit is 1, and the total area in blue is the relative probability that the first digit is 8.


For the left distribution, the size of the areas of red and blue are approximately proportional to the widths of each red and blue bar. Therefore the numbers drawn from this distribution will approximately follow Benford's law. On the other hand, for the right distribution, the ratio of the areas of red and blue is very different from the ratio of the widths of each red and blue bar. Rather, the relative areas of red and blue are determined more by the height of the bars than the widths. The heights, unlike the widths, do not satisfy the universal relationship of Benford's law; instead, they are determined entirely by the shape of the distribution in question. Accordingly, the first digits in this distribution do not satisfy Benford's law at all.
Thus, real-world distributions that span several orders of magnitude rather smoothly like the left distribution (e.g. income distributions, or populations of towns and cities) are likely to satisfy Benford's law to a very good approximation. On the other hand, a distribution that covers only one or two orders of magnitude, like the right distribution (e.g. heights of human adults, or IQ scores) is unlikely to satisfy Benford's law well.
Distributions that exactly satisfy Benford's law
Some well-known infinite integer sequenceInteger sequence
In mathematics, an integer sequence is a sequence of integers.An integer sequence may be specified explicitly by giving a formula for its nth term, or implicitly by giving a relationship between its terms...
s satisfy Benford's law exactly (in the asymptotic limit as more and more terms of the sequence are included). Among these are the Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s, the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s, the powers of 2, and the powers of almost any other number.
Likewise, some continuous processes satisfy Benford's law exactly (in the asymptotic limit as the process continues longer and longer). One is an exponential growth
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
or decay process: If a quantity is exponentially increasing or decreasing in time, then the percentage of time that it has each first digit satisfies Benford's law asymptotically (i.e., more and more accurately as the process continues for more and more time).
Generalization to digits beyond the first
It is possible to extend the law to digits beyond the first. In particular, the probability of encountering a number starting with the string of digits n is given by:
(For example, the probability that a number starts with the digits 3, 1, 4 is log10(1 + 1/314) ≈ 0.0014.) This result can be used to find the probability that a particular digit occurs at a given position within a number. For instance, the probability that a "2" is encountered as the second digit is

And the probability that d (d = 0, 1, ..., 9) is encountered as the n-th (n > 1) digit is

The distribution of the n-th digit, as n increases, rapidly approaches a uniform distribution with 10% for each of the ten digits.
In practice, applications of Benford's law for fraud detection routinely use more than the first digit.
General audience
- Benford Online Bibliography, an online bibliographic database on Benford's Law.
- Following Benford's Law, or Looking Out for No. 1, 1998 article from The New York TimesThe New York TimesThe New York Times is an American daily newspaper founded and continuously published in New York City since 1851. The New York Times has won 106 Pulitzer Prizes, the most of any news organization...
. - A further five numbers: number 1 and Benford's law, BBCBBCThe British Broadcasting Corporation is a British public service broadcaster. Its headquarters is at Broadcasting House in the City of Westminster, London. It is the largest broadcaster in the world, with about 23,000 staff...
radio segment by Simon SinghSimon SinghSimon Lehna Singh, MBE is a British author who has specialised in writing about mathematical and scientific topics in an accessible manner.... - From Benford to Erdös, Radio segment from the Radiolab program
- Looking out for number one by Jon Walthoe, Robert Hunt and Mike Pearson, Plus Magazine, September 1999
- Video showing Benford's Law applied to Web Data (incl. Minnesota Lakes, US Census Data and Digg Statistics)
- An illustration of Benford's Law, showing first-digit distributions of various sequences evolve over time, interactive.
- Testing Benford's Law An open source project showing Benford's Law in action against publicly available datasets.
More mathematical
- Benford’s law, Zipf’s law, and the Pareto distribution by Terence TaoTerence TaoTerence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...
- Country Data and Benford's Law, Benford's Law from Ratios of Random Numbers at Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. - Benford's Law Solved with Digital Signal Processing



