Logarithmic scale
Encyclopedia
A logarithmic scale is a scale of measurement using the logarithm
of a physical quantity
instead of the quantity itself.
A simple example is a chart whose vertical axis increments are labeled 1, 10, 100, 1000, instead of 1, 2, 3, 4. Each unit increase on the logarithmic scale thus represents an exponential
increase in the underlying quantity for the given base (10, in this case).
Presentation of data on a logarithmic scale can be helpful when the data cover a large range of values. The use of the logarithms of the values rather than the actual values reduces a wide range to a more manageable size. Some of our sense
s operate in a logarithmic fashion (Weber–Fechner law
), which makes logarithmic scales for these input quantities especially appropriate. In particular our sense of hearing
perceives equal ratios of frequencies as equal differences in pitch. In addition, studies of young children in an isolated tribe have shown logarithmic scales to be the most natural display of numbers by humans.
Some logarithmic scales were designed such that large values (or ratios) of the underlying quantity correspond to small values of the logarithmic measure. Examples of such scales are:
function. In this article, a given logarithmic unit will be denoted using the notation [log n], where n is a positive real number, and [log ] here denotes the indefinite logarithm
function Log.
and entropy
, such as the bit
[log 2] and the byte
8[log 2] = [log 256], also the nat
[log e] and the ban
[log 10]; units of relative signal strength magnitude such as the decibel
0.1[log 10] and bel [log 10], neper
[log e], and other logarithmic-scale units such as the Richter scale point [log 10] or (more generally) the corresponding order-of-magnitude unit sometimes referred to as a factor of ten or decade
(here meaning [log 10], not 10 years).
the logarithms of any given number a to two different bases (here b and c) differ only by the constant factor logc b. This constant factor can be considered to represent the conversion factor for converting a numerical representation of the pure (indefinite) logarithmic quantity Log(a) from one arbitrary unit of measurement (the [log c] unit) to another (the [log b] unit), since
For example, Boltzmann's standard definition of entropy S = k ln W (where W is the number of ways of arranging a system and k is Boltzmann's constant) can also written more simply as just S = Log(W), where "Log" here denotes the indefinite logarithm
, and we let k = [log e]; that is, we identify the physical entropy unit k with the mathematical unit [log e]. This identity works because
Thus, we can interpret Boltzmann's constant as being simply the expression (in terms of more standard physical units) of the abstract logarithmic unit [log e] that is needed to convert the dimensionless pure-number quantity ln W (which uses an arbitrary choice of base, namely e) to the more fundamental pure logarithmic quantity Log(W), which implies no particular choice of base, and thus no particular choice of physical unit for measuring entropy.
A logarithmic scale is also a graphical scale on one or both sides of a graph where a number x is printed at a distance c·log(x) from the point marked with the number 1. A slide rule
has logarithmic scales, and nomogram
s often employ logarithmic scales. On a logarithmic scale an equal difference in order of magnitude
is represented by an equal distance. The geometric mean
of two numbers is midway between the numbers.
Logarithmic graph paper
, before the advent of computer graphics, was a basic scientific tool. Plots on paper with one log scale can show up exponential laws, and on log-log paper power law
s, as straight lines (see semi-log graph, log-log graph
).
In the first case, plotting the equation on a semilog scale (log Y versus X) gives: log Y = −aX, which is linear.
In the second case, plotting the equation on a log-log scale (log Y versus log X) gives: log Y = b log X, which is linear.
When values that span large ranges need to be plotted, a logarithmic scale can provide a means of viewing the data that allows the values to be determined from the graph. The logarithmic scale is marked off in distances proportional to the logarithms of the values being represented. For example, in the figure below, for both plots, y has the values of: 1, 2, 3, 4, 5, 6, 7, 8, 9 10, 20, 30, 40, 50, 60, 70, 80, 90 and 100. For the plot on the left, the log10 of the values of y are plotted on a linear scale. Thus the first value is log10(1) = 0; the second value is log10(2) = 0.301; the 3rd value is log10(3) = 0.4771; the 4th value is log10(4) = 0.602, and so on. The plot on the right uses logarithmic (or log, as it is also referred to) scaling on the vertical axis. Note that values where the exponent term is close to an integral fraction of 10 (0.1, 0.2, 0.3, etc.) are shown as 10 raised to the power that yields the original value of y. These are shown for y = 2, 4, 8, 10, 20, 40, 80 and 100.
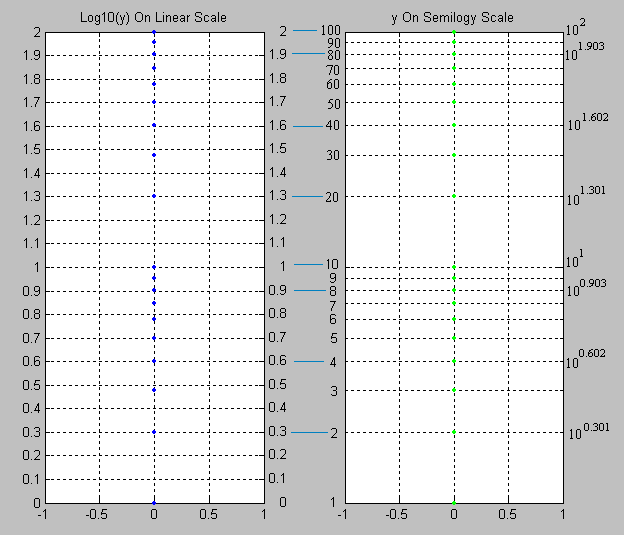
Note that for y = 2 and 20, y = 100.301 and 101.301; for y = 4 and 40, y = 100.602 and 101.602. This is due to the law that
So, knowing log10(2) = 0.301, the rest can be derived:
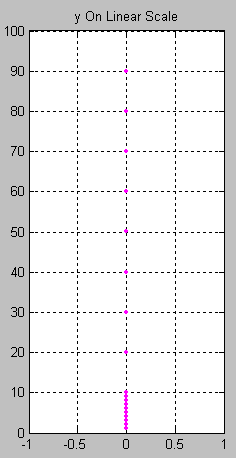
Note that the values of y are easily picked off the above figure. By comparison, values of y less than 10 are difficult to determine from the figure below, where they are plotted on a linear scale, thus confirming the earlier assertion that values spanning large ranges are more easily read from a logarithmically scaled graph.
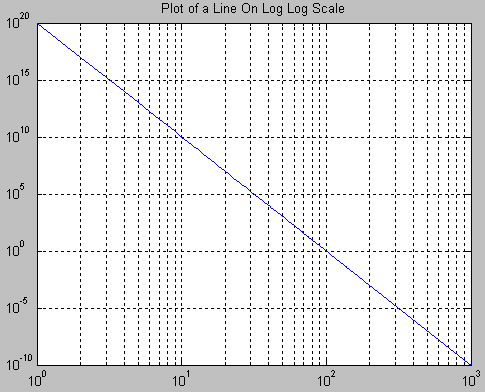If both the vertical and horizontal axis of a plot is scaled logarithmically, the plot is referred to as a log-log plot. The equation for a line on a log-log scale would be:
where m is the slope and b is the intercept point on the log plot.
To find the slope of the plot, two points are selected on the x-axis, say x1 and x2. Using the above equation:
and
The slope m is found taking the difference:
where F1 is shorthand for F ( x1 ) and the same for F2. The figure at right illustrates the formula. Notice that the slope in the example of the figure is negative. The formula also provides a negative slope, as can be seen from the following property of the logarithm:
which leads to
Notice that 10log10(F1) = F1. Therefore, the logs can be inverted to find:
or
which means that
In other words, F is proportional to x to the power of the slope of the straight line of its log-log graph. Specifically, a straight line on a log-log plot containing points (F0, x0) and (F1, x1) will have the function:
Of course, the inverse is true too: any function of the form
will have a straight line as its log-log graph representation, where the slope of the line is m.
or abscissa
is scaled logarithmically, the plot is referred to as a semi logarithmic plot. The equation for a line with an ordinate axis logarithmically scaled would be:
The equation of a line on a plot where the abscissa axis is scaled logarithmically would be
Example: What is the value that lies halfway between the 10 and 100 decades on a logarithmic axis? Since it is the halfway point that is of interest, the quotient of steps 1 and 2 is 0.5. The nearest decade line with lower value is 10, so the halfway point's value is (100.5) × 10 = 101.5 ≈ 31.62.
To estimate where a value lies within a decade on a logarithmic axis, use the following method:
Example: To determine where 17 is located on a logarithmic axis, first use a ruler to measure the distance between 10 and 100. If the measurement is 30mm on a ruler (it can vary — ensure that the same scale is used throughout the rest of the process).
x = 17 is then 6.9mm after x = 10 (along the x-axis).
Y is the unknown ordinate. Using cross-multiplication, Y can be calculated and is equal to 6.
In logarithmic interpolation, a ratio of logarithmic values is set equal to a ratio of linear values. For example, consider a log base 10 scale graph of paper reams sold per day measuring 19 1/32 inches from 1 to 10. How many reams were sold in a day if the value on the graph is 11 1/32 between 1 and 10? In order to solve this problem, it is necessary to use a basic logarithmic definition:
Decade lines, those values that denote powers of the log base, are also important in logarithmic interpolation. Locate the lower decade line. It is the closest decade line to the number you are evaluating that is lower than that number. Decade lines begin at 1. The next decade line is the first power of your log base. For log base 10, the first decade line is 1, the second is 10, the third is 100, and so on.
The ratio of linear values is the number of units from the lower decade line to the value of interest (11 1/32 in this example, since the lower decade line in this example is 1) divided by the total number of units between the lower decade line and the upper decade line (the upper decade line is 10 in this example). Therefore, the linear ratio is:
Notice that the units (1/32 inch) are removed from the equation because both measurements are in the same units. Conversion to a single unit before calculating the ratio is required if the measurements were made in different units.
The logarithmic ratio uses the same graphical measurements as the linear ratio. The difference between the log of the upper decade line (10) and the log of the lower decade line (1) represents the same graphical distance as the total number of units between the two decade lines in the linear ratio (19 1/32nds of an inch). Therefore, the lower part of the logarithmic ratio (the bottom part of the fraction) is:
The upper part of the logarithmic ratio (the top part of the fraction) represents the same graphical distance as the number of units between the value of interest (number of reams of paper sold) and the lower decade line in linear ratio (11 1/32nds of an inch). The unknown in this ratio is the value of interest, which we will call X. Therefore, the top part of the fraction is:
The logarithmic ratio is:
The linear ratio is equal to the logarithmic ratio. Therefore, the equation required to determine the number of paper reams sold in a particular day is:
This equation can be rewritten using the logarithmic definition mentioned above:
log(10) = 1, therefore:
In order to remove the "log" from the right side of the equation, both sides must be used as exponents for the number 10, meaning 10 to the power of 11/19 and 10 to the power of log(X/1). The "log" function and the "10 to the power of" function are reciprocal and cancel each other out, leaving:
Now both sides must be multiplied by 1. While the 1 drops out of this equation, it is important to note that the number X is divided by is the value of the lower decade line. If this example involved values between 10 and 100, the equation would include X/10 instead of X/1.
X = 3.793 reams of paper.
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of a physical quantity
Physical quantity
A physical quantity is a physical property of a phenomenon, body, or substance, that can be quantified by measurement.-Definition of a physical quantity:Formally, the International Vocabulary of Metrology, 3rd edition defines quantity as:...
instead of the quantity itself.
A simple example is a chart whose vertical axis increments are labeled 1, 10, 100, 1000, instead of 1, 2, 3, 4. Each unit increase on the logarithmic scale thus represents an exponential
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
increase in the underlying quantity for the given base (10, in this case).
Presentation of data on a logarithmic scale can be helpful when the data cover a large range of values. The use of the logarithms of the values rather than the actual values reduces a wide range to a more manageable size. Some of our sense
Sense
Senses are physiological capacities of organisms that provide inputs for perception. The senses and their operation, classification, and theory are overlapping topics studied by a variety of fields, most notably neuroscience, cognitive psychology , and philosophy of perception...
s operate in a logarithmic fashion (Weber–Fechner law
Weber–Fechner law
The Weber–Fechner law is a confusing term, because it combines two different laws. Some authors use the term to mean Weber's law, and others Fechner's law. Fechner himself added confusion to the literature by calling his own law Weber's law...
), which makes logarithmic scales for these input quantities especially appropriate. In particular our sense of hearing
Hearing (sense)
Hearing is the ability to perceive sound by detecting vibrations through an organ such as the ear. It is one of the traditional five senses...
perceives equal ratios of frequencies as equal differences in pitch. In addition, studies of young children in an isolated tribe have shown logarithmic scales to be the most natural display of numbers by humans.
Definition and base
Logarithmic scales are either defined for ratios of the underlying quantity, or one has to agree to measure the quantity in fixed units. Deviating from these units means that the logarithmic measure will change by an additive constant. The base of the logarithm also has to be specified, unless the scale's value is considered to be a dimensional quantity expressed in generic (indefinite-base) logarithmic units.Example scales
On most logarithmic scales, small values (or ratios) of the underlying quantity correspond to negative values of the logarithmic measure. Well-known examples of such scales are:- Richter magnitude scaleRichter magnitude scaleThe expression Richter magnitude scale refers to a number of ways to assign a single number to quantify the energy contained in an earthquake....
and moment magnitude scaleMoment magnitude scaleThe moment magnitude scale is used by seismologists to measure the size of earthquakes in terms of the energy released. The magnitude is based on the seismic moment of the earthquake, which is equal to the rigidity of the Earth multiplied by the average amount of slip on the fault and the size of...
(MMS) for strength of earthquakes and movementMotion (physics)In physics, motion is a change in position of an object with respect to time. Change in action is the result of an unbalanced force. Motion is typically described in terms of velocity, acceleration, displacement and time . An object's velocity cannot change unless it is acted upon by a force, as...
in the earthEarthEarth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
. - ban and decibanBan (information)A ban, sometimes called a hartley or a dit , is a logarithmic unit which measures information or entropy, based on base 10 logarithms and powers of 10, rather than the powers of 2 and base 2 logarithms which define the bit. As a bit corresponds to a binary digit, so a ban is a decimal digit...
, for information or weight of evidence; - bel and decibelDecibelThe decibel is a logarithmic unit that indicates the ratio of a physical quantity relative to a specified or implied reference level. A ratio in decibels is ten times the logarithm to base 10 of the ratio of two power quantities...
and neperNeperThe neper is a logarithmic unit for ratios of measurements of physical field and power quantities, such as gain and loss of electronic signals. It has the unit symbol Np. The unit's name is derived from the name of John Napier, the inventor of logarithms...
for acoustic power (loudness) and electric power; - centCent (music)The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each...
, minor secondMinor secondIn modern Western tonal music theory a minor second is the interval between two notes on adjacent staff positions, or having adjacent note letters, whose alterations cause them to be one semitone or half-step apart, such as B and C or C and D....
, major secondMajor secondIn Western music theory, a major second is a musical interval spanning two semitones, and encompassing two adjacent staff positions . For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff postions...
, and octaveOctaveIn music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
for the relative pitch of notes in musicMusicMusic is an art form whose medium is sound and silence. Its common elements are pitch , rhythm , dynamics, and the sonic qualities of timbre and texture...
; - logitLogitThe logit function is the inverse of the sigmoidal "logistic" function used in mathematics, especially in statistics.Log-odds and logit are synonyms.-Definition:The logit of a number p between 0 and 1 is given by the formula:...
for oddsOddsThe odds in favor of an event or a proposition are expressed as the ratio of a pair of integers, which is the ratio of the probability that an event will happen to the probability that it will not happen...
in statisticsStatisticsStatistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
; - Palermo Technical Impact Hazard ScalePalermo Technical Impact Hazard ScaleThe Palermo Technical Impact Hazard Scale is a logarithmic scale used by astronomers to rate the potential hazard of impact of a near-earth object . It combines two types of data—probability of impact, and estimated kinetic yield—into a single "hazard" value...
; - Logarithmic timelineLogarithmic timelineA logarithmic timeline is a timeline laid out according to a logarithmic scale. This necessarily implies a zero point and an infinity point, neither of which can be displayed. The most natural zero point is the Big Bang, looking forward, but the most common is the ever-changing present, looking...
; - counting f-stops for ratios of photographic exposure;
- rating low probabilities by the number of 'nines' in the decimal expansion of the probability of their not happening: for example, a system which will fail with a probability of 10−5 is 99.999% reliable: "five nines".
- EntropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
in thermodynamicsThermodynamicsThermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
. - InformationInformationInformation in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...
in information theoryInformation theoryInformation theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
. - Particle Size Distribution curves of soil
Some logarithmic scales were designed such that large values (or ratios) of the underlying quantity correspond to small values of the logarithmic measure. Examples of such scales are:
- pHPHIn chemistry, pH is a measure of the acidity or basicity of an aqueous solution. Pure water is said to be neutral, with a pH close to 7.0 at . Solutions with a pH less than 7 are said to be acidic and solutions with a pH greater than 7 are basic or alkaline...
for acidity and alkalinity; - stellar magnitude scaleApparent magnitudeThe apparent magnitude of a celestial body is a measure of its brightness as seen by an observer on Earth, adjusted to the value it would have in the absence of the atmosphere...
for brightness of starStarA star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s; - Krumbein scale for particle sizeParticle size (grain size)Particle size, also called grain size, refers to the diameter of individual grains of sediment, or the lithified particles in clastic rocks. The term may also be applied to other granular materials. This is different from the crystallite size, which is the size of a single crystal inside the...
in geologyGeologyGeology is the science comprising the study of solid Earth, the rocks of which it is composed, and the processes by which it evolves. Geology gives insight into the history of the Earth, as it provides the primary evidence for plate tectonics, the evolutionary history of life, and past climates...
. - Absorbance of light by transparent samples.
Logarithmic units
Logarithmic units are abstract mathematical units that can be used to express any quantities (physical or mathematical) that are defined on a logarithmic scale, that is, as being proportional to the value of a logarithmLogarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
function. In this article, a given logarithmic unit will be denoted using the notation [log n], where n is a positive real number, and [log ] here denotes the indefinite logarithm
Indefinite logarithm
The indefinite logarithm of a positive number n is the logarithm without regard to any particular base: it is a function , not a number...
function Log.
Examples
Examples of logarithmic units include common units of informationInformation
Information in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...
and entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
, such as the bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
[log 2] and the byte
Byte
The byte is a unit of digital information in computing and telecommunications that most commonly consists of eight bits. Historically, a byte was the number of bits used to encode a single character of text in a computer and for this reason it is the basic addressable element in many computer...
8[log 2] = [log 256], also the nat
Nat (information)
A nat is a logarithmic unit of information or entropy, based on natural logarithms and powers of e, rather than the powers of 2 and base 2 logarithms which define the bit. The nat is the natural unit for information entropy...
[log e] and the ban
Ban (information)
A ban, sometimes called a hartley or a dit , is a logarithmic unit which measures information or entropy, based on base 10 logarithms and powers of 10, rather than the powers of 2 and base 2 logarithms which define the bit. As a bit corresponds to a binary digit, so a ban is a decimal digit...
[log 10]; units of relative signal strength magnitude such as the decibel
Decibel
The decibel is a logarithmic unit that indicates the ratio of a physical quantity relative to a specified or implied reference level. A ratio in decibels is ten times the logarithm to base 10 of the ratio of two power quantities...
0.1[log 10] and bel [log 10], neper
Neper
The neper is a logarithmic unit for ratios of measurements of physical field and power quantities, such as gain and loss of electronic signals. It has the unit symbol Np. The unit's name is derived from the name of John Napier, the inventor of logarithms...
[log e], and other logarithmic-scale units such as the Richter scale point [log 10] or (more generally) the corresponding order-of-magnitude unit sometimes referred to as a factor of ten or decade
Decade (log scale)
One decade is a factor of 10 difference between two numbers measured on a logarithmic scale. It is especially useful when referring to frequencies and when describing frequency response of electronic systems, such as audio amplifiers and filters.-Calculations:The factor-of-ten in a decade can be...
(here meaning [log 10], not 10 years).
Motivation
The motivation behind the concept of logarithmic units is that defining a quantity on a logarithmic scale in terms of a logarithm to a specific base amounts to making a (totally arbitrary) choice of a unit of measurement for that quantity, one that corresponds to the specific (and equally arbitrary) logarithm base that was selected. Due to the identity
the logarithms of any given number a to two different bases (here b and c) differ only by the constant factor logc b. This constant factor can be considered to represent the conversion factor for converting a numerical representation of the pure (indefinite) logarithmic quantity Log(a) from one arbitrary unit of measurement (the [log c] unit) to another (the [log b] unit), since
For example, Boltzmann's standard definition of entropy S = k ln W (where W is the number of ways of arranging a system and k is Boltzmann's constant) can also written more simply as just S = Log(W), where "Log" here denotes the indefinite logarithm
Indefinite logarithm
The indefinite logarithm of a positive number n is the logarithm without regard to any particular base: it is a function , not a number...
, and we let k = [log e]; that is, we identify the physical entropy unit k with the mathematical unit [log e]. This identity works because
Thus, we can interpret Boltzmann's constant as being simply the expression (in terms of more standard physical units) of the abstract logarithmic unit [log e] that is needed to convert the dimensionless pure-number quantity ln W (which uses an arbitrary choice of base, namely e) to the more fundamental pure logarithmic quantity Log(W), which implies no particular choice of base, and thus no particular choice of physical unit for measuring entropy.
Graphic representation
Slide rule
The slide rule, also known colloquially as a slipstick, is a mechanical analog computer. The slide rule is used primarily for multiplication and division, and also for functions such as roots, logarithms and trigonometry, but is not normally used for addition or subtraction.Slide rules come in a...
has logarithmic scales, and nomogram
Nomogram
A nomogram, nomograph, or abac is a graphical calculating device developed by P.E. Elyasberg, a two-dimensional diagram designed to allow the approximate graphical computation of a function: it uses a coordinate system other than Cartesian coordinates...
s often employ logarithmic scales. On a logarithmic scale an equal difference in order of magnitude
Order of magnitude
An order of magnitude is the class of scale or magnitude of any amount, where each class contains values of a fixed ratio to the class preceding it. In its most common usage, the amount being scaled is 10 and the scale is the exponent being applied to this amount...
is represented by an equal distance. The geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
of two numbers is midway between the numbers.
Logarithmic graph paper
Graph paper
Graph paper, graphing paper, grid paper or millimeter paper is writing paper that is printed with fine lines making up a regular grid. The lines are often used as guides for plotting mathematical functions or experimental data and drawing diagrams. It is commonly found in mathematics and...
, before the advent of computer graphics, was a basic scientific tool. Plots on paper with one log scale can show up exponential laws, and on log-log paper power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
s, as straight lines (see semi-log graph, log-log graph
Log-log graph
In science and engineering, a log-log graph or log-log plot is a two-dimensional graph of numerical data that uses logarithmic scales on both the horizontal and vertical axes...
).
Logarithmic and semi-logarithmic plots and equations of lines
Log and semilog scales are best used to view two types of equations (for ease, the natural base 'e' is used):
In the first case, plotting the equation on a semilog scale (log Y versus X) gives: log Y = −aX, which is linear.
In the second case, plotting the equation on a log-log scale (log Y versus log X) gives: log Y = b log X, which is linear.
When values that span large ranges need to be plotted, a logarithmic scale can provide a means of viewing the data that allows the values to be determined from the graph. The logarithmic scale is marked off in distances proportional to the logarithms of the values being represented. For example, in the figure below, for both plots, y has the values of: 1, 2, 3, 4, 5, 6, 7, 8, 9 10, 20, 30, 40, 50, 60, 70, 80, 90 and 100. For the plot on the left, the log10 of the values of y are plotted on a linear scale. Thus the first value is log10(1) = 0; the second value is log10(2) = 0.301; the 3rd value is log10(3) = 0.4771; the 4th value is log10(4) = 0.602, and so on. The plot on the right uses logarithmic (or log, as it is also referred to) scaling on the vertical axis. Note that values where the exponent term is close to an integral fraction of 10 (0.1, 0.2, 0.3, etc.) are shown as 10 raised to the power that yields the original value of y. These are shown for y = 2, 4, 8, 10, 20, 40, 80 and 100.
Note that for y = 2 and 20, y = 100.301 and 101.301; for y = 4 and 40, y = 100.602 and 101.602. This is due to the law that
So, knowing log10(2) = 0.301, the rest can be derived:
Note that the values of y are easily picked off the above figure. By comparison, values of y less than 10 are difficult to determine from the figure below, where they are plotted on a linear scale, thus confirming the earlier assertion that values spanning large ranges are more easily read from a logarithmically scaled graph.
Log-log plots
where m is the slope and b is the intercept point on the log plot.
Slope of a log-log plot
and
The slope m is found taking the difference:
where F1 is shorthand for F ( x1 ) and the same for F2. The figure at right illustrates the formula. Notice that the slope in the example of the figure is negative. The formula also provides a negative slope, as can be seen from the following property of the logarithm:
Finding the function from the log-log plot
The above procedure now is reversed to find the form of the function F(x) using its (assumed) known log-log plot. To find the function F, pick some fixed point (x0, F0), where F0 is shorthand for F(x0), somewhere on the straight line in the above graph, and further some other arbitrary point (x1, F1) on the same graph. Then from the slope formula above:
which leads to
Notice that 10log10(F1) = F1. Therefore, the logs can be inverted to find:
or
which means that
In other words, F is proportional to x to the power of the slope of the straight line of its log-log graph. Specifically, a straight line on a log-log plot containing points (F0, x0) and (F1, x1) will have the function:
Of course, the inverse is true too: any function of the form
will have a straight line as its log-log graph representation, where the slope of the line is m.
Semi logarithmic plots
If only the ordinateOrdinate
In mathematics, ordinate refers to that element of an ordered pair which is plotted on the vertical axis of a two-dimensional Cartesian coordinate system, as opposed to the abscissa...
or abscissa
Abscissa
In mathematics, abscissa refers to that element of an ordered pair which is plotted on the horizontal axis of a two-dimensional Cartesian coordinate system, as opposed to the ordinate...
is scaled logarithmically, the plot is referred to as a semi logarithmic plot. The equation for a line with an ordinate axis logarithmically scaled would be:
The equation of a line on a plot where the abscissa axis is scaled logarithmically would be
Estimating values in a diagram with logarithmic scale
One method for accurate determination of values on a logarithmic axis is as follows:- Measure the distance from the point on the scale to the closest decade line with lower value with a ruler.
- Divide this distance by the length of a decade (the length between two decade lines).
- The value of your chosen point is now the value of the nearest decade line with lower value times 10a where a is the value found in step 2.
Example: What is the value that lies halfway between the 10 and 100 decades on a logarithmic axis? Since it is the halfway point that is of interest, the quotient of steps 1 and 2 is 0.5. The nearest decade line with lower value is 10, so the halfway point's value is (100.5) × 10 = 101.5 ≈ 31.62.
To estimate where a value lies within a decade on a logarithmic axis, use the following method:
- Measure the distance between consecutive decades with a ruler. You can use any units provided that you are consistent.
- Take the log (value of interest/nearest lower value decade) multiplied by the number determined in step one.
- Using the same units as in step 1, count as many units as resulted from step 2, starting at the lower decade.
Example: To determine where 17 is located on a logarithmic axis, first use a ruler to measure the distance between 10 and 100. If the measurement is 30mm on a ruler (it can vary — ensure that the same scale is used throughout the rest of the process).
- [log (17/10)] × 30 = 6.9
x = 17 is then 6.9mm after x = 10 (along the x-axis).
Logarithmic interpolation
Interpolating logarithmic values is very similar to interpolating linear values. In linear interpolation, values are determined through equal ratios. For example, in linear interpolation, a line that increases one ordinate (y-value) for every two abscissa (x-value) has a ratio (also known as slope or rise-over-run) of 1/2. In order to determine the ordinate or abscissa of a particular point, you must know the other value. The calculation of the ordinate corresponding to an abscissa of 12 in the example below is as follows:- 1/2 = Y/12
Y is the unknown ordinate. Using cross-multiplication, Y can be calculated and is equal to 6.
In logarithmic interpolation, a ratio of logarithmic values is set equal to a ratio of linear values. For example, consider a log base 10 scale graph of paper reams sold per day measuring 19 1/32 inches from 1 to 10. How many reams were sold in a day if the value on the graph is 11 1/32 between 1 and 10? In order to solve this problem, it is necessary to use a basic logarithmic definition:
- log(A) − log(B) = log(A/B)
Decade lines, those values that denote powers of the log base, are also important in logarithmic interpolation. Locate the lower decade line. It is the closest decade line to the number you are evaluating that is lower than that number. Decade lines begin at 1. The next decade line is the first power of your log base. For log base 10, the first decade line is 1, the second is 10, the third is 100, and so on.
The ratio of linear values is the number of units from the lower decade line to the value of interest (11 1/32 in this example, since the lower decade line in this example is 1) divided by the total number of units between the lower decade line and the upper decade line (the upper decade line is 10 in this example). Therefore, the linear ratio is:
- 11/19
Notice that the units (1/32 inch) are removed from the equation because both measurements are in the same units. Conversion to a single unit before calculating the ratio is required if the measurements were made in different units.
The logarithmic ratio uses the same graphical measurements as the linear ratio. The difference between the log of the upper decade line (10) and the log of the lower decade line (1) represents the same graphical distance as the total number of units between the two decade lines in the linear ratio (19 1/32nds of an inch). Therefore, the lower part of the logarithmic ratio (the bottom part of the fraction) is:
- log(10) − log(1)
The upper part of the logarithmic ratio (the top part of the fraction) represents the same graphical distance as the number of units between the value of interest (number of reams of paper sold) and the lower decade line in linear ratio (11 1/32nds of an inch). The unknown in this ratio is the value of interest, which we will call X. Therefore, the top part of the fraction is:
- log(X) − log(1)
The logarithmic ratio is:
- [log(X) − log(1)]/[log(10) − log(1)]
The linear ratio is equal to the logarithmic ratio. Therefore, the equation required to determine the number of paper reams sold in a particular day is:
- 11/19 = [log(X) − log(1)]/[log(10) − log(1)]
This equation can be rewritten using the logarithmic definition mentioned above:
- 11/19 = log(X/1)/log(10)
log(10) = 1, therefore:
- 11/19 = log(X/1)
In order to remove the "log" from the right side of the equation, both sides must be used as exponents for the number 10, meaning 10 to the power of 11/19 and 10 to the power of log(X/1). The "log" function and the "10 to the power of" function are reciprocal and cancel each other out, leaving:
- 1011/19 = X/1
Now both sides must be multiplied by 1. While the 1 drops out of this equation, it is important to note that the number X is divided by is the value of the lower decade line. If this example involved values between 10 and 100, the equation would include X/10 instead of X/1.
- 1011/19 = X
X = 3.793 reams of paper.
See also
- Preferred numberPreferred numberIn industrial design, preferred numbers are standard guidelines for choosing exact product dimensions within a given set of constraints....
- LogarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
- Indefinite logarithmIndefinite logarithmThe indefinite logarithm of a positive number n is the logarithm without regard to any particular base: it is a function , not a number...
- EntropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
Units of information
- bitBitA bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
[log 2] - byteByteThe byte is a unit of digital information in computing and telecommunications that most commonly consists of eight bits. Historically, a byte was the number of bits used to encode a single character of text in a computer and for this reason it is the basic addressable element in many computer...
8[log 2] = [log 256] - natNat (information)A nat is a logarithmic unit of information or entropy, based on natural logarithms and powers of e, rather than the powers of 2 and base 2 logarithms which define the bit. The nat is the natural unit for information entropy...
[log e] - banBan (information)A ban, sometimes called a hartley or a dit , is a logarithmic unit which measures information or entropy, based on base 10 logarithms and powers of 10, rather than the powers of 2 and base 2 logarithms which define the bit. As a bit corresponds to a binary digit, so a ban is a decimal digit...
[log 10]
Units of relative signal strength
- belBelBel can mean:* bel , a unit of ratio used in acoustics, electronics, etc. A derived unit of 1 decibel = 0.1 B is often used.* Bel , a Semitic deity * Belenus aka Bel; a Celtic deity...
[log 10] - decibelDecibelThe decibel is a logarithmic unit that indicates the ratio of a physical quantity relative to a specified or implied reference level. A ratio in decibels is ten times the logarithm to base 10 of the ratio of two power quantities...
0.1[log 10] - neperNeperThe neper is a logarithmic unit for ratios of measurements of physical field and power quantities, such as gain and loss of electronic signals. It has the unit symbol Np. The unit's name is derived from the name of John Napier, the inventor of logarithms...
[log e]