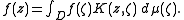Bergman kernel
Encyclopedia
In the mathematical
study of several complex variables
, the Bergman kernel, named after Stefan Bergman
, is a reproducing kernel for the Hilbert space
of all square integrable holomorphic function
s on a domain D in Cn.
In detail, let L2(D)
be the Hilbert space of square integrable functions on D, and let L2,h(D) denote the subspace consisting of holomorphic functions in D: that is,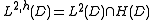
where H(D) is the space of holomorphic functions in D. Then L2,h(D) is a Hilbert space: it is a closed
linear subspace of L2(D), and therefore complete in its own right. This follows from the fundamental estimate, that for a holomorphic square-integrable function ƒ in D
for every compact subset K of D. Thus convergence of a sequence of holomorphic functions in L2(D) implies also compact convergence
, and so the limit function is also holomorphic.
Another consequence of is that, for each z ∈ D, the evaluation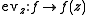
is a continuous linear functional on L2,h(D). By the Riesz representation theorem
, this functional can be represented as the inner product with an element of L2,h(D), which is to say that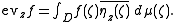
The Bergman kernel K is defined by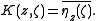
The kernel K(z,ζ) holomorphic in z and antiholomorphic in ζ, and satisfies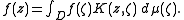
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
study of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, the Bergman kernel, named after Stefan Bergman
Stefan Bergman
Stefan Bergman was a Polish-born American mathematician whose primary work was in complex analysis. He is best known for the kernel function he discovered while at Berlin University in 1922. This function is known today as the Bergman kernel...
, is a reproducing kernel for the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of all square integrable holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s on a domain D in Cn.
In detail, let L2(D)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
be the Hilbert space of square integrable functions on D, and let L2,h(D) denote the subspace consisting of holomorphic functions in D: that is,
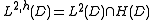
where H(D) is the space of holomorphic functions in D. Then L2,h(D) is a Hilbert space: it is a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
linear subspace of L2(D), and therefore complete in its own right. This follows from the fundamental estimate, that for a holomorphic square-integrable function ƒ in D
for every compact subset K of D. Thus convergence of a sequence of holomorphic functions in L2(D) implies also compact convergence
Compact convergence
In mathematics compact convergence is a type of convergence which generalizes the idea of uniform convergence. It is associated with the compact-open topology.-Definition:...
, and so the limit function is also holomorphic.
Another consequence of is that, for each z ∈ D, the evaluation
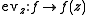
is a continuous linear functional on L2,h(D). By the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
, this functional can be represented as the inner product with an element of L2,h(D), which is to say that
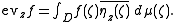
The Bergman kernel K is defined by
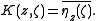
The kernel K(z,ζ) holomorphic in z and antiholomorphic in ζ, and satisfies