
Bergman metric
Encyclopedia
In differential geometry, the Bergman metric is a Hermitian metric that can be defined on certain types of complex manifold
. It is so called because it is derived from the Bergman kernel
, both of which are named for Stefan Bergman
.
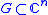 be a domain and let
be a domain and let 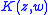 be the Bergman kernel
be the Bergman kernel
on G. We define a Hermitian metric on the tangent bundle
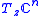 by
by
for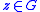 . Then the length of a tangent vector
. Then the length of a tangent vector 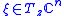 is
is
given by

This metric is called the Bergman metric on G.
The length of a (piecewise) C1 curve
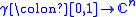 is
is
then computed as
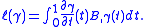
The distance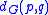 of two points
of two points 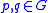 is then defined as
is then defined as

The distance dG is called the Bergman distance.
The Bergman metric is in fact a positive definite matrix at each point if G is a bounded domain. More importantly, the distance dG is invariant under
biholomorphic mappings of G to another domain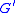 . That is if f
. That is if f
is a biholomorphism of G and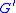 , then
, then 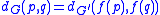 .
.
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
. It is so called because it is derived from the Bergman kernel
Bergman kernel
In the mathematical study of several complex variables, the Bergman kernel, named after Stefan Bergman, is a reproducing kernel for the Hilbert space of all square integrable holomorphic functions on a domain D in Cn....
, both of which are named for Stefan Bergman
Stefan Bergman
Stefan Bergman was a Polish-born American mathematician whose primary work was in complex analysis. He is best known for the kernel function he discovered while at Berlin University in 1922. This function is known today as the Bergman kernel...
.
Definition
Let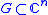 be a domain and let
be a domain and let 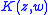 be the Bergman kernel
be the Bergman kernelon G. We define a Hermitian metric on the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
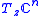 by
by
for
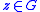 . Then the length of a tangent vector
. Then the length of a tangent vector 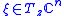 is
isgiven by

This metric is called the Bergman metric on G.
The length of a (piecewise) C1 curve
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
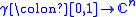 is
isthen computed as
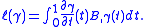
The distance
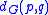 of two points
of two points 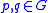 is then defined as
is then defined as
The distance dG is called the Bergman distance.
The Bergman metric is in fact a positive definite matrix at each point if G is a bounded domain. More importantly, the distance dG is invariant under
biholomorphic mappings of G to another domain
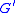 . That is if f
. That is if fis a biholomorphism of G and
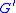 , then
, then 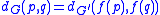 .
.

