
Besov space
Encyclopedia
In mathematics
, the Besov space (named after Oleg Vladimirovich Besov)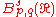 is a complete quasinormed space which is a Banach space
is a complete quasinormed space which is a Banach space
when It, as well as the similarly defined Triebel–Lizorkin space
It, as well as the similarly defined Triebel–Lizorkin space
, serve to generalize more elementary function spaces and are effective at measuring (in a sense) smoothness properties of functions.
Let
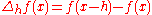
and the modulus of continuity
is defined by
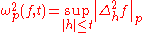
Let with
with  , the Besov space
, the Besov space
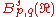 contains all functions
contains all functions  such that
such that
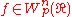 and
and
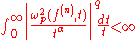
The Besov space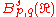 is equipped with the norm
is equipped with the norm
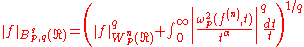
If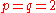 , the Besov spaces
, the Besov spaces 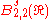 coincide with the more classical Sobolev spaces
coincide with the more classical Sobolev spaces 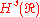 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Besov space (named after Oleg Vladimirovich Besov)
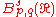 is a complete quasinormed space which is a Banach space
is a complete quasinormed space which is a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
when
 It, as well as the similarly defined Triebel–Lizorkin space
It, as well as the similarly defined Triebel–Lizorkin spaceTriebel–Lizorkin space
In the mathematical discipline known as functional analysis, a Triebel–Lizorkin space is a generalization of many standard function spaces such as Lp spaces and Sobolev spaces. It is named after Hans Triebel and Petr Ivanovich Lizorkin....
, serve to generalize more elementary function spaces and are effective at measuring (in a sense) smoothness properties of functions.
Let
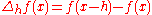
and the modulus of continuity
Modulus of continuity
In mathematical analysis, a modulus of continuity is a function\omega:[0,\infty]\to[0,\infty]used to measure quantitatively the uniform continuity of functions. So, a function f:I\to\R admits \omega as a modulus of continuity if and only if|f-f|\leq\omega,for all x and y in the domain of f...
is defined by
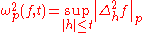
Let
 with
with  , the Besov space
, the Besov space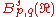 contains all functions
contains all functions  such that
such that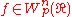 and
and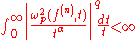
The Besov space
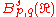 is equipped with the norm
is equipped with the norm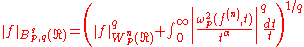
If
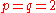 , the Besov spaces
, the Besov spaces 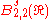 coincide with the more classical Sobolev spaces
coincide with the more classical Sobolev spaces 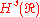 .
.

