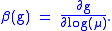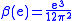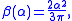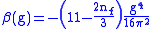Beta-function
Encyclopedia
In theoretical physics
, specifically quantum field theory
, a beta function β(g) encodes the dependence of a coupling parameter
, g, on the energy scale,
of a given physical process.
It is defined by the relation:
This dependence on the energy scale is known as the running of the coupling parameter, and theory of this kind of scale-dependence in quantum field theory is described by the renormalization group
.
. Almost all scale-invariant QFTs are also conformally invariant
. The study of such theories is conformal field theory
.
The coupling parameters of a quantum field theory can run even if the corresponding classical field theory
is scale-invariant. In this case, the non-zero beta function tells us that the classical scale invariance is anomalous
.
, where one assumes that the coupling parameters are small. One can then make an expansion in powers of the coupling parameters and truncate the higher-order terms (also known as higher loop
contributions, due to the number of loops in the corresponding Feynman graph
s).
Here are some examples of beta functions computed in perturbation theory:
(QED) is
or
written in terms of the fine structure constant,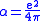
.
This beta function tells us that the coupling increases with increasing energy scale, and QED becomes strongly coupled at high energy. In fact, the coupling apparently becomes infinite at some finite energy, resulting in a Landau pole
. However, one cannot expect the perturbative beta function to give accurate results at strong coupling, and so it is likely that the Landau pole is an artifact of applying perturbation theory in a situation where it is no longer valid.
with
flavours is
or
written in terms of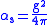
.
If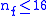
, this beta function tells us that the coupling decreases with increasing energy scale, a phenomenon known as asymptotic freedom
. Conversely, the coupling increases with decreasing energy scale. This means that the coupling becomes large at low energies, and one can no longer rely on perturbation theory.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, specifically quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, a beta function β(g) encodes the dependence of a coupling parameter
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
, g, on the energy scale,
of a given physical process.It is defined by the relation:
This dependence on the energy scale is known as the running of the coupling parameter, and theory of this kind of scale-dependence in quantum field theory is described by the renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
.
Scale invariance
If the beta functions of a quantum field theory vanish, usually at particular values of the coupling parameters, then the theory is said to be scale-invariantScale invariance
In physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...
. Almost all scale-invariant QFTs are also conformally invariant
Conformal symmetry
In theoretical physics, conformal symmetry is a symmetry under dilatation and under the special conformal transformations...
. The study of such theories is conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
.
The coupling parameters of a quantum field theory can run even if the corresponding classical field theory
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
is scale-invariant. In this case, the non-zero beta function tells us that the classical scale invariance is anomalous
Conformal anomaly
Conformal anomaly is an anomaly i.e. a quantum phenomenon that breaks the conformal symmetry of the classical theory.A classically conformal theory is a theory which, when placed on a surface with arbitrary background metric, has an action that is invariant under rescalings of the background metric...
.
Examples
Beta functions are usually computed in some kind of approximation scheme. An example is perturbation theoryPerturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
, where one assumes that the coupling parameters are small. One can then make an expansion in powers of the coupling parameters and truncate the higher-order terms (also known as higher loop
Feynman graph
A Feynman graph is a graph suitable to be a Feynman diagram in a particular application of quantum field theory.A Feynman graph is a graph suitable to be a Feynman diagram in a particular application of quantum field theory.A Feynman graph is a graph suitable to be a Feynman diagram in a particular...
contributions, due to the number of loops in the corresponding Feynman graph
Feynman graph
A Feynman graph is a graph suitable to be a Feynman diagram in a particular application of quantum field theory.A Feynman graph is a graph suitable to be a Feynman diagram in a particular application of quantum field theory.A Feynman graph is a graph suitable to be a Feynman diagram in a particular...
s).
Here are some examples of beta functions computed in perturbation theory:
Quantum electrodynamics
The one-loop beta function in quantum electrodynamicsQuantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
(QED) is
or
written in terms of the fine structure constant,
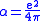.This beta function tells us that the coupling increases with increasing energy scale, and QED becomes strongly coupled at high energy. In fact, the coupling apparently becomes infinite at some finite energy, resulting in a Landau pole
Landau pole
In physics, the Landau pole is the momentum scale at which the coupling constant of a quantum field theory becomes infinite...
. However, one cannot expect the perturbative beta function to give accurate results at strong coupling, and so it is likely that the Landau pole is an artifact of applying perturbation theory in a situation where it is no longer valid.
Quantum chromodynamics
The one-loop beta function in quantum chromodynamicsQuantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
with
flavours is
or
,
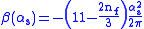written in terms of
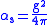.If
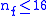, this beta function tells us that the coupling decreases with increasing energy scale, a phenomenon known as asymptotic freedomAsymptotic freedom
In physics, asymptotic freedom is a property of some gauge theories that causes interactions between particles to become arbitrarily weak at energy scales that become arbitrarily large, or, equivalently, at length scales that become arbitrarily small .Asymptotic freedom is a feature of quantum...
. Conversely, the coupling increases with decreasing energy scale. This means that the coupling becomes large at low energies, and one can no longer rely on perturbation theory.