
Beta negative binomial distribution
Encyclopedia
In probability theory
, a beta negative binomial distribution is the probability distribution
of a discrete random variable
X equal to the number of failures in needed to get n successes in a sequence of independent Bernoulli trial
s where the probability p of success on each trial is constant within any given experiment but is itself a random variable following a beta distribution, varying between different experiments. Thus the distribution is a compound probability distribution
.
This distribution has also been called both the inverse Markov-Pólya distribution and the generalized Waring distribution. A shifted form of the distribution has been called the beta-Pascal distribution.
If parameters of the beta distribution are α and β , and if
where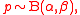
then the marginal distribution of X is a beta negative binomial distribution:
In the above, NB(n, p) is the negative binomial distribution
and B(α, β) is the beta distribution.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a beta negative binomial distribution is the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of a discrete random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X equal to the number of failures in needed to get n successes in a sequence of independent Bernoulli trial
Bernoulli trial
In the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
s where the probability p of success on each trial is constant within any given experiment but is itself a random variable following a beta distribution, varying between different experiments. Thus the distribution is a compound probability distribution
Compound probability distribution
In probability theory, a compound probability distribution is the probability distribution that results from assuming that a random variable is distributed according to some parametrized distribution F with an unknown parameter θ that is distributed according to some other distribution G, and then...
.
This distribution has also been called both the inverse Markov-Pólya distribution and the generalized Waring distribution. A shifted form of the distribution has been called the beta-Pascal distribution.
If parameters of the beta distribution are α and β , and if

where
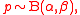
then the marginal distribution of X is a beta negative binomial distribution:

In the above, NB(n, p) is the negative binomial distribution
Negative binomial distribution
In probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
and B(α, β) is the beta distribution.

