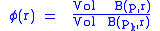In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Bishop–Gromov inequality is a comparison theorem in Riemannian geometry, named after Richard L. Bishop and Mikhail Gromov. It is closely related to Myers' theorem, and is the key point in the proof of Gromov's compactness theorem

Gromov's compactness theorem (geometry)

In Riemannian geometry, Gromov's compactness theorem states thatthe set of Riemannian manifolds of a given dimension, with Ricci curvature ≥ c and diameter ≤ D is relatively compact in the Gromov-Hausdorff metric. It was proved by Mikhail Gromov....

.

Statement

Let be a complete n-dimensional Riemannian manifold whose Ricci curvature

Ricci curvature

In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...

 satisfies the lower bound

for a constant ρ ∈ R. Further, let M_kⁿ be the n-dimensional simply connected Riemannian space form

Space form

In mathematics, a space form is a complete Riemannian manifold M of constant sectional curvature K. The three obvious examples are Euclidean n-space, the n-dimensional sphere, and hyperbolic space, although a space form need not be simply connected.-Reduction to generalized crystallography:It is a...

 of constant sectional curvature

Sectional curvature

In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...

 k = (n-1) ρ (i.e. constant Ricci curvature ρ), so M_kⁿ is an n-sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

 if k > 0, it is an n-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

 if k = 0, and it is an n-dimensional hyperbolic space

Hyperbolic space

In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...

 if k < 0. Denote by B(p, r) the ball of radius r around a point p , defined with respect to the Riemannian distance function.

Then for any p ∈ M and p_k ∈ M_kⁿ the function

is non-increasing on (0, ∞). Furthermore, as r goes to zero, the ratio approaches one, so together with the monotonicty this implies that