
Bispectrum
Encyclopedia
In mathematics
, in the area of statistical analysis, the bispectrum is a statistic used to search for nonlinear interactions. The Fourier transform
of the second-order cumulant
, i.e., the autocorrelation
function, is the traditional power spectrum. The Fourier transform of C3(t1, t2) (third-order cumulant
-generating function) is called the bispectrum or bispectral density. Applying the convolution theorem
allows fast calculation of the bispectrum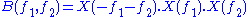 .
.
Bispectra fall in the category of higher-order spectra, or polyspectra and provide supplementary information to the power spectrum. The third order polyspectrum (bispectrum) is the easiest to compute, and hence the most popular.
A statistic defined analogously is the bispectral coherency or bicoherence.
Bispectrum and bicoherence
may be applied to the case of non-linear interactions of a continuous spectrum of propagating waves in one dimension .
Bispectral measurements have been carried out for EEG
signals monitoring.
In seismology
, signals rarely have adequate duration for making sensible bispectral estimates from time averages.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of statistical analysis, the bispectrum is a statistic used to search for nonlinear interactions. The Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the second-order cumulant
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
, i.e., the autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
function, is the traditional power spectrum. The Fourier transform of C3(t1, t2) (third-order cumulant
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
-generating function) is called the bispectrum or bispectral density. Applying the convolution theorem
Convolution theorem
In mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
allows fast calculation of the bispectrum
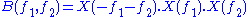 .
.Bispectra fall in the category of higher-order spectra, or polyspectra and provide supplementary information to the power spectrum. The third order polyspectrum (bispectrum) is the easiest to compute, and hence the most popular.
A statistic defined analogously is the bispectral coherency or bicoherence.
Bispectrum and bicoherence
Bicoherence
In mathematics, in the area of statistical analysis, bicoherence is a squared normalised version of the bispectrum. The bicoherence takes values bounded between 0 and 1, which make it a convenient measure for quantifying the extent of phase coupling in a signal. It is also known as bispectral...
may be applied to the case of non-linear interactions of a continuous spectrum of propagating waves in one dimension .
Bispectral measurements have been carried out for EEG
Electroencephalography
Electroencephalography is the recording of electrical activity along the scalp. EEG measures voltage fluctuations resulting from ionic current flows within the neurons of the brain...
signals monitoring.
In seismology
Seismology
Seismology is the scientific study of earthquakes and the propagation of elastic waves through the Earth or through other planet-like bodies. The field also includes studies of earthquake effects, such as tsunamis as well as diverse seismic sources such as volcanic, tectonic, oceanic,...
, signals rarely have adequate duration for making sensible bispectral estimates from time averages.

