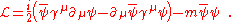Bispinor
Encyclopedia
In physics
, bispinor is a four-component object which transforms under the (½,0)⊕(0,½) representation
of the covariance group
of special relativity
(see, e.g.). Bispinors are used to describe relativistic spin-½
quantum fields
.
In the Weyl basis a bispinor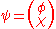
consists of two (two-component) Weyl spinors and
and  which transform, correspondingly, under (½,0) and (0,½) representations of the
which transform, correspondingly, under (½,0) and (0,½) representations of the 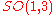 group (the Lorentz group without parity transformations). Under parity transformation the Weyl spinors transform into each other.
group (the Lorentz group without parity transformations). Under parity transformation the Weyl spinors transform into each other.
The Dirac bispinor is connected with the Weyl bispinor by a unitary transformation to the Dirac basis,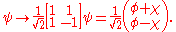
The Dirac basis is the one most widely used in the literature.
A bilinear form of bispinors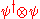 can be reduced to five irreducible (under the Lorentz group) objects:
can be reduced to five irreducible (under the Lorentz group) objects:
where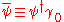 and
and 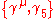 are the gamma matrices.
are the gamma matrices.
A suitable Lagrangian (the Euler-Lagrange equation
of which is the Dirac equation
) for the relativistic spin-½ field is given as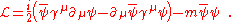
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, bispinor is a four-component object which transforms under the (½,0)⊕(0,½) representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the covariance group
Covariance group
In physics, covariance group is a group of coordinate transformations between admissible frames of reference . The frames are assumed to provide equivalent description of physical phenomena...
of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
(see, e.g.). Bispinors are used to describe relativistic spin-½
Spin-½
In quantum mechanics, spin is an intrinsic property of all elementary particles. Fermions, the particles that constitute ordinary matter, have half-integer spin. Spin-½ particles constitute an important subset of such fermions. All known elementary fermions have a spin of ½.- Overview :Particles...
quantum fields
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
.
In the Weyl basis a bispinor
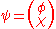
consists of two (two-component) Weyl spinors
 and
and  which transform, correspondingly, under (½,0) and (0,½) representations of the
which transform, correspondingly, under (½,0) and (0,½) representations of the 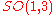 group (the Lorentz group without parity transformations). Under parity transformation the Weyl spinors transform into each other.
group (the Lorentz group without parity transformations). Under parity transformation the Weyl spinors transform into each other.The Dirac bispinor is connected with the Weyl bispinor by a unitary transformation to the Dirac basis,
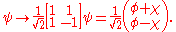
The Dirac basis is the one most widely used in the literature.
A bilinear form of bispinors
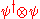 can be reduced to five irreducible (under the Lorentz group) objects:
can be reduced to five irreducible (under the Lorentz group) objects:
- scalarScalar (physics)In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
,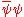 ;
; - pseudo-scalar,
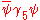 ;
; - vectorFour-vectorIn the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
,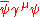 ;
; - pseudo-vector,
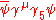 ;
; - antisymmetric tensor,
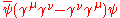 ,
,
where
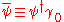 and
and 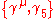 are the gamma matrices.
are the gamma matrices.A suitable Lagrangian (the Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
of which is the Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
) for the relativistic spin-½ field is given as