
Blattner's conjecture
Encyclopedia
In mathematics
, Blattner's conjecture or Blattner's formula is a description of the discrete series representation
s of a general semisimple group G in terms of their restricted representation
s to a maximal compact subgroup
K (their so-called K-types). Harish-Chandra orally attributed the conjecture to Robert J Blattner, who did not publish it. It first appeared in print in , though mentioned a special case of it slightly earlier. proved Blattner's formula in some special cases, showed that Blattner's formula gave an upper bound for the multiplicities of K-representations, proved Blattner's conjecture for groups whose symmetric space is Hermitian, and proved Blattner's conjecture for linear semisimple groups.
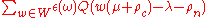
where
Blattner's formula is what one gets by formally restricting the Harish-Chandra character formula for a discrete series representation to the maximal torus of a maximal compact group. The problem in proving the Blattner formula is that this only gives the character on the regular elements of the maximal torus, and one also needs to control its behavior on the singular elements. For non-discrete irreducible representations the formal restriction of Harish-Chandra's character formula need not give the decomposition under the maximal compact subgroup: for example, for the principal series representations of SL2 the character is identically zero on the non-singular elements of the maximal compact subgroup, but the representation is not zero on this subgroup. In this case the character is a distribution on the maximal compact subgroup with support on the singular elements.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Blattner's conjecture or Blattner's formula is a description of the discrete series representation
Discrete series representation
In mathematics, a discrete series representation is an irreducible unitary representation of a locally compact topological group G that is a subrepresentation of the left regular representation of G on L²...
s of a general semisimple group G in terms of their restricted representation
Restricted representation
In mathematics, restriction is a fundamental construction in representation theory of groups. Restriction forms a representation of a subgroup from a representation of the whole group. Often the restricted representation is simpler to understand...
s to a maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
K (their so-called K-types). Harish-Chandra orally attributed the conjecture to Robert J Blattner, who did not publish it. It first appeared in print in , though mentioned a special case of it slightly earlier. proved Blattner's formula in some special cases, showed that Blattner's formula gave an upper bound for the multiplicities of K-representations, proved Blattner's conjecture for groups whose symmetric space is Hermitian, and proved Blattner's conjecture for linear semisimple groups.
Statement
Blattner's formula says that if a discrete series representation with infinitesimal character λ is restricted to a maximal compact subgroup K, then the representation of K with highest weight μ occurs with multiplicity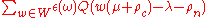
where
- Q is the number of ways a vector can be written as a sum of non-compact positive roots
- W is the Weyl group
- ρc is half the sum of the compact roots
- ρn is half the sum of the non-compact roots
- ε is the sign character of W.
Blattner's formula is what one gets by formally restricting the Harish-Chandra character formula for a discrete series representation to the maximal torus of a maximal compact group. The problem in proving the Blattner formula is that this only gives the character on the regular elements of the maximal torus, and one also needs to control its behavior on the singular elements. For non-discrete irreducible representations the formal restriction of Harish-Chandra's character formula need not give the decomposition under the maximal compact subgroup: for example, for the principal series representations of SL2 the character is identically zero on the non-singular elements of the maximal compact subgroup, but the representation is not zero on this subgroup. In this case the character is a distribution on the maximal compact subgroup with support on the singular elements.

