
Discrete series representation
Encyclopedia
In mathematics
, a discrete series representation is an irreducible unitary representation
of a locally compact topological group
G that is a subrepresentation of the left regular representation of G on L²(G). In the Plancherel measure
, such representations have positive measure.
The name comes from the fact that they are exactly the representations that occur discretely in the decomposition of the regular representation.
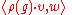
with v, w non-zero vectors is square-integrable on G, with respect to Haar measure
.
When G is unimodular, the discrete series representation has a formal dimension d, with the property that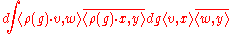
for v, w, x, y in the representation. When G is compact this coincides with the dimension when the Haar measure on G is normalized so that G has measure 1.
K. In other words, a maximal torus
T in K must be a Cartan subgroup
in G. (This result required that the center of G be finite, ruling out groups such as the simply connected cover of SL2(R).) It applies in particular to special linear group
s; of these only SL2(R) has a discrete series (for this, see the representation theory of SL2(R)).
Harish-Chandra's classification of the discrete series representations of a semisimple connected Lie group is given as follows.
If L is the weight lattice of the maximal torus T, a sublattice of it where t is the Lie algebra of T, then there is a discrete series representation for every vector v of
where ρ is the Weyl vector of G, that is not orthogonal to any root of G. Every discrete series representation occurs in this way. Two such vectors v correspond to the same discrete series representation if and only if they are conjugate under the Weyl group
WK of the maximal compact subgroup K. If we fix a fundamental chamber for the Weyl group of K, then the discrete series representation are in 1:1 correspondence with the vectors of L + ρ in this Weyl chamber that are not orthogonal to any root of G. The infinitesimal character of the highest weight representation is given by v (mod the Weyl group WG of G) under the Harish-Chandra correspondence identifying infinitesimal characters of G with points of
So for each discrete series representation, there are exactly
discrete series representations with the same infinitesimal character.
Harish-Chandra went on to prove an analogue for these representations of the Weyl character formula
. In the case where G is not compact, the representations have infinite dimension, and the notion of character is therefore more subtle to define since it is a Schwartz distribution (represented by a locally integrable function), with singularities.
The character is given on the maximal torus T by
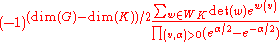
When G is compact this reduces to the Weyl character formula, with v = λ + ρ for λ the highest weight of the irreducible representation (where the product is over roots α having positive inner product with the vector v).
Harish-Chandra's regularity theorem
implies that the character of a discrete series representation is a locally integrable function on the group.
series representation if and only if they are conjugate under the Weyl group of K. Just as for discrete series representations v gives the infinitesimal character. There are at most |WG|/|WK| limit of discrete series representations with any given infinitesimal character.
Limit of discrete series representations are tempered representation
s, which means roughly that they only just fail to be discrete series representations
constructed most of the discrete series representations in the case when the symmetric space of G is hermitean. constructed many of the discrete series representations for arbitrary G. conjectured, and proved, a geometric analogue of the Borel–Bott–Weil theorem, for the discrete series, using L2 cohomology instead of the coherent sheaf cohomology used in the compact case.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a discrete series representation is an irreducible unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of a locally compact topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
G that is a subrepresentation of the left regular representation of G on L²(G). In the Plancherel measure
Plancherel measure
In mathematics, Plancherel measure is a probability measure defined on the set of irreducible representations of a finite group G. In some cases the term Plancherel measure is applied specifically in the context of the group G being the finite symmetric group S_n – see below...
, such representations have positive measure.
The name comes from the fact that they are exactly the representations that occur discretely in the decomposition of the regular representation.
Properties
If G is unimodular, an irreducible unitary representation ρ of G is in the discrete series if and only if one matrix coefficientMatrix coefficient
In mathematics, a matrix coefficient is a function on agroup of a special form, which depends on a linear representation of the group and additional data...
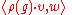
with v, w non-zero vectors is square-integrable on G, with respect to Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
.
When G is unimodular, the discrete series representation has a formal dimension d, with the property that
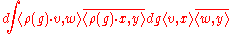
for v, w, x, y in the representation. When G is compact this coincides with the dimension when the Haar measure on G is normalized so that G has measure 1.
Semisimple groups
classified the discrete series representations of connected semisimple groups G. In particular, such a group has discrete series representations if and only if it has the same rank as a maximal compact subgroupMaximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
K. In other words, a maximal torus
Maximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
T in K must be a Cartan subgroup
Cartan subgroup
In mathematics, a Cartan subgroup of a Lie group or algebraic group G is one of the subgroups whose Lie algebrais a Cartan subalgebra. The dimension of a Cartan subgroup, and therefore of a Cartan subalgebra, is the rank of G.-Conventions:...
in G. (This result required that the center of G be finite, ruling out groups such as the simply connected cover of SL2(R).) It applies in particular to special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
s; of these only SL2(R) has a discrete series (for this, see the representation theory of SL2(R)).
Harish-Chandra's classification of the discrete series representations of a semisimple connected Lie group is given as follows.
If L is the weight lattice of the maximal torus T, a sublattice of it where t is the Lie algebra of T, then there is a discrete series representation for every vector v of
- L + ρ,
where ρ is the Weyl vector of G, that is not orthogonal to any root of G. Every discrete series representation occurs in this way. Two such vectors v correspond to the same discrete series representation if and only if they are conjugate under the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
WK of the maximal compact subgroup K. If we fix a fundamental chamber for the Weyl group of K, then the discrete series representation are in 1:1 correspondence with the vectors of L + ρ in this Weyl chamber that are not orthogonal to any root of G. The infinitesimal character of the highest weight representation is given by v (mod the Weyl group WG of G) under the Harish-Chandra correspondence identifying infinitesimal characters of G with points of
- t⊗C/WG.
So for each discrete series representation, there are exactly
- |WG|/|WK|
discrete series representations with the same infinitesimal character.
Harish-Chandra went on to prove an analogue for these representations of the Weyl character formula
Weyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
. In the case where G is not compact, the representations have infinite dimension, and the notion of character is therefore more subtle to define since it is a Schwartz distribution (represented by a locally integrable function), with singularities.
The character is given on the maximal torus T by
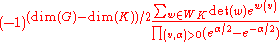
When G is compact this reduces to the Weyl character formula, with v = λ + ρ for λ the highest weight of the irreducible representation (where the product is over roots α having positive inner product with the vector v).
Harish-Chandra's regularity theorem
Harish-Chandra's regularity theorem
In mathematics, Harish-Chandra's regularity theorem, introduced by , states that every invariant eigendistribution on a semisimple Lie group, and in particular every character of an irreducible unitary representation on a Hilbert space, is given by a locally integrable function...
implies that the character of a discrete series representation is a locally integrable function on the group.
Limit of discrete series representations
Points v in the coset L + ρ orthogonal to roots of G do not correspond to discrete series representations, but those not orthogonal to roots of K are related to certain irreducible representations called limit of discrete series representations. There is such a representation for every pair (v,C) where v is a vector of L + ρ orthogonal to some root of G but no orthogonal to any root of K corresponding to a wall of C, and C is a Weyl chamber of G containing v. (In the case of discrete series representations there is only one Weyl chamber containing v so it is not necessary to include it explicitly.) Two pairs (v,C) give the same limit of discreteseries representation if and only if they are conjugate under the Weyl group of K. Just as for discrete series representations v gives the infinitesimal character. There are at most |WG|/|WK| limit of discrete series representations with any given infinitesimal character.
Limit of discrete series representations are tempered representation
Tempered representation
In mathematics, a tempered representation of a linear semisimple Lie group is a representation that has a basis whose matrix coefficients lie in the Lp spacefor any ε > 0.-Formulation:...
s, which means roughly that they only just fail to be discrete series representations
Constructions of the discrete series
Harish-Chandra's original construction of the discrete series was not very explicit. Several authors later found more explicit realizations of the discrete series.constructed most of the discrete series representations in the case when the symmetric space of G is hermitean. constructed many of the discrete series representations for arbitrary G. conjectured, and proved, a geometric analogue of the Borel–Bott–Weil theorem, for the discrete series, using L2 cohomology instead of the coherent sheaf cohomology used in the compact case.
- An application of the index theorem, constructed all the discrete series representations in spaces of harmonic spinors. Unlike most of the previous constructions of representations, the work of Atiyah and Schmid did not use Harish-Chandra's existence results in their proofs.
- Discrete series representations can also be constructed by cohomological parabolic induction using Zuckerman functorZuckerman functorIn mathematics, a Zuckerman functor is used to construct representations of real reductive Lie groups from representations of Levi subgroups. They were introduced by Gregg Zuckerman...
s.
See also
- Blattner's conjectureBlattner's conjectureIn mathematics, Blattner's conjecture or Blattner's formula is a description of the discrete series representations of a general semisimple group G in terms of their restricted representations to a maximal compact subgroup K . Harish-Chandra orally attributed the conjecture to Robert J Blattner,...
- Holomorphic discrete series representationHolomorphic discrete series representationIn mathematics, a holomorphic discrete series representation is a discrete series representation of a semisimple Lie group that can be represented in a natural way as a Hilbert space of holomorphic functions. The simple Lie groups with holomorphic discrete series are those whose symmetric space is ...
- Quaternionic discrete series representationQuaternionic discrete series representationIn mathematics, a quaternionic discrete series representation is a discrete series representation of a semisimple Lie group G associated with a quaternionic structure on the symmetric space of G. They were introduced by ....

