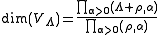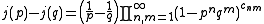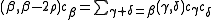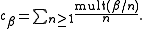Weyl character formula
Encyclopedia
In mathematics
, the Weyl character formula in representation theory
describes the character
s of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by .
By definition, the character of a representation r of G is the trace of r(g), as a function of a group element g in G. The irreducible representations in this case are all finite-dimensional (this is part of the Peter-Weyl theorem); so the notion of trace is the usual one from linear algebra. Knowledge of the character χ of r is a good substitute for r itself, and can have algorithmic content. Weyl's formula is a closed formula for the χ, in terms of other objects constructed from G and its Lie algebra
. The representations in question here are complex, and so without loss of generality are unitary representation
s; irreducible therefore means the same as indecomposable, i.e. not a direct sum of two subrepresentations.
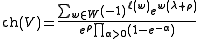
where
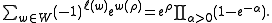
For special unitary groups, this is equivalent to the expression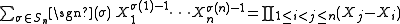
for the Vandermonde determinant.
for the dimension
of a finite dimensional representation VΛ with highest weight Λ. (As usual, ρ is the Weyl vector and the products run over positive roots α.) The specialization is not completely trivial, because both
the numerator and denominator of the Weyl character formula vanish to high order at the identity element, so it is necessary to take a limit of the trace of an element tending to the identity.
's formula is a recursive formula for the weight multiplicities that is equivalent to the Weyl character formula, but is sometimes
easier to use for calculations as there can be far fewer terms to sum. It states
where
s, when it is known as the Weyl–Kac character formula. Similarly there is a denominator identity for Kac–Moody algebra
s, which in the case of the affine Lie algebras is equivalent to the Macdonald
identities. In the simplest case of the affine Lie algebra of type A1 this is the Jacobi triple product identity
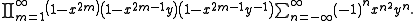
The character formula can also be extended to integrable highest weight representations of generalized Kac–Moody algebra
s, when the character is given by
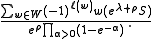
Here S is a correction term given in terms of the imaginary simple roots by
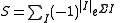
where the sum runs over all finite subsets I of the imaginary simple roots which are pairwise orthogonal and orthogonal to the highest weight λ, and |I| is the cardinality of I and ΣI is the sum of the elements of I.
The denominator formula for the monster Lie algebra
is the product formula
for the elliptic modular function j.
Peterson gave a recursion formula for the multiplicities mult(β) of the roots β of a symmetrizable (generalized) Kac–Moody algebra, which is equivalent to the Weyl–Kac denominator formula, but easier to use for calculations:
where the sum is over positive roots γ, δ, and
. Suppose
is an irreducible, admissible representation
of a real, reductive group G with infinitesimal character
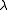. Let 
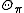be the Harish-Chandra character
of
; it is given by integration against an analytic function
on the regular set. If H is a Cartan subgroup
of G and H' is the set of regular elements in H, then
Here
and the rest of the notation is as above.
The coefficients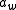
are still not well understood. Results on these coefficients may be found in papers of Herb, Adams, Schmid, and Schmid-Vilonen among others.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Weyl character formula in representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
describes the character
Character (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
s of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by .
By definition, the character of a representation r of G is the trace of r(g), as a function of a group element g in G. The irreducible representations in this case are all finite-dimensional (this is part of the Peter-Weyl theorem); so the notion of trace is the usual one from linear algebra. Knowledge of the character χ of r is a good substitute for r itself, and can have algorithmic content. Weyl's formula is a closed formula for the χ, in terms of other objects constructed from G and its Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. The representations in question here are complex, and so without loss of generality are unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s; irreducible therefore means the same as indecomposable, i.e. not a direct sum of two subrepresentations.
Statement of Weyl character formula
The character of an irreducible representation V of a compact Lie group G is given by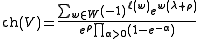where
- ρ is the Weyl vector of the group G, defined to be half the sum of the positive roots;
- W is the Weyl groupWeyl groupIn mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
; - λ is the highest weight of the irreducible representation V;
- α runs over the positive roots of the Lie group.
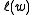is the length of the Weyl group element, defined to be the minimal number of reflections with respect to simple roots such that 
equals the product of those reflections.
Weyl denominator formula
In the special case of the trivial 1 dimensional representation the character is 1, so the Weyl character formula becomes the Weyl denominator formula: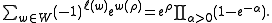For special unitary groups, this is equivalent to the expression
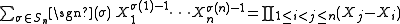
for the Vandermonde determinant.
Weyl dimension formula
By specialization to the trace of the identity element, Weyl's character formula gives the Weyl dimension formula
for the dimension
of a finite dimensional representation VΛ with highest weight Λ. (As usual, ρ is the Weyl vector and the products run over positive roots α.) The specialization is not completely trivial, because both
the numerator and denominator of the Weyl character formula vanish to high order at the identity element, so it is necessary to take a limit of the trace of an element tending to the identity.
Freudenthal's formula
Hans FreudenthalHans Freudenthal
Hans Freudenthal was a Dutch mathematician. He made substantial contributions to algebraic topology and also took an interest in literature, philosophy, history and mathematics education....
's formula is a recursive formula for the weight multiplicities that is equivalent to the Weyl character formula, but is sometimes
easier to use for calculations as there can be far fewer terms to sum. It states
where
- Λ is a highest weight,
- λ is some other weight,
- dim Vλ is the multiplicity of the weight λ
- ρ is the Weyl vector
- The first sum is over all positive roots α.
Weyl–Kac character formula
The Weyl character formula also holds for integrable highest weight representations of Kac–Moody algebraKac–Moody algebra
In mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix...
s, when it is known as the Weyl–Kac character formula. Similarly there is a denominator identity for Kac–Moody algebra
Kac–Moody algebra
In mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix...
s, which in the case of the affine Lie algebras is equivalent to the Macdonald
Ian G. Macdonald
Ian Grant Macdonald is a British mathematician known for his contributions to symmetric functions, special functions, Lie algebra theory and other aspects of algebraic combinatorics ....
identities. In the simplest case of the affine Lie algebra of type A1 this is the Jacobi triple product identity
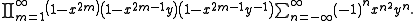
The character formula can also be extended to integrable highest weight representations of generalized Kac–Moody algebra
Generalized Kac–Moody algebra
In mathematics, a generalized Kac–Moody algebra is a Lie algebra that is similar to aKac–Moody algebra, except that it is allowed to have imaginary simple roots.Generalized Kac–Moody algebras are also sometimes called GKM algebras,...
s, when the character is given by
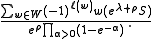
Here S is a correction term given in terms of the imaginary simple roots by
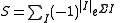
where the sum runs over all finite subsets I of the imaginary simple roots which are pairwise orthogonal and orthogonal to the highest weight λ, and |I| is the cardinality of I and ΣI is the sum of the elements of I.
The denominator formula for the monster Lie algebra
Monster Lie algebra
In mathematics, the monster Lie algebra is an infinitedimensional generalized Kac–Moody algebra acted on by the monster group, which was used to prove the monstrous moonshine conjectures.- Structure :...
is the product formula
for the elliptic modular function j.
Peterson gave a recursion formula for the multiplicities mult(β) of the roots β of a symmetrizable (generalized) Kac–Moody algebra, which is equivalent to the Weyl–Kac denominator formula, but easier to use for calculations:
where the sum is over positive roots γ, δ, and
Harish-Chandra Character Formula
Harish-Chandra showed that Weyl's character formula admits a generalization to representations of a real, reductive groupReductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
. Suppose
is an irreducible, admissible representationAdmissible representation
In mathematics, admissible representations are a well-behaved class of representations used in the representation theory of reductive Lie groups and locally compact totally disconnected groups. They were introduced by Harish-Chandra....
of a real, reductive group G with infinitesimal character
Infinitesimal character
In mathematics, the infinitesimal character of an irreducible representation ρ of a semisimple Lie group G on a vector space V is, roughly speaking, a mapping to scalars that encodes the process of first differentiating and then diagonalizing the representation...
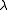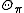. Let be the Harish-Chandra characterHarish-Chandra character
In mathematics, the Harish-Chandra character, named after Harish-Chandra, of a representation of a semisimple Lie group G on a Hilbert space H is a distribution on the group G that is analogous to the character of a finite dimensional representation of a compact group.-Definition:Suppose that π...
of
; it is given by integration against an analytic functionAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
on the regular set. If H is a Cartan subgroup
Cartan subgroup
In mathematics, a Cartan subgroup of a Lie group or algebraic group G is one of the subgroups whose Lie algebrais a Cartan subalgebra. The dimension of a Cartan subgroup, and therefore of a Cartan subalgebra, is the rank of G.-Conventions:...
of G and H' is the set of regular elements in H, then
Here
- W is the complex Weyl group of
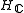with respect to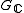 
-
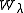is the stabilizer of 
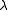in W
and the rest of the notation is as above.
The coefficients
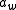are still not well understood. Results on these coefficients may be found in papers of Herb, Adams, Schmid, and Schmid-Vilonen among others.