
Harish-Chandra character
Encyclopedia
In mathematics, the Harish-Chandra character, named after Harish-Chandra
, of a representation of a semisimple Lie group G on a Hilbert space
H is a distribution
on the group G that is analogous to the character of a finite dimensional representation of a compact group
.
of G on a Hilbert space H.
If f is a compactly supported smooth function
on the group G, then the operator on H

is of trace class
, and the distribution
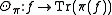
is called the character (or global character or Harish-Chandra character) of the representation.
The character Θπ is a distribution on G that is invariant under conjugation, and is an eigendistribution of the center of
the universal enveloping algebra
of G, in other words an invariant eigendistribution, with eigenvalue the infinitesimal character
of the representation π.
Harish-Chandra's regularity theorem
states that any invariant eigendistribution, and in particular any character of an irreducible unitary representation on a Hilbert space, is given by a locally integrable function
.
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
, of a representation of a semisimple Lie group G on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H is a distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
on the group G that is analogous to the character of a finite dimensional representation of a compact group
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
.
Definition
Suppose that π is an irreducible unitary representationUnitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of G on a Hilbert space H.
If f is a compactly supported smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
on the group G, then the operator on H

is of trace class
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
, and the distribution
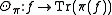
is called the character (or global character or Harish-Chandra character) of the representation.
The character Θπ is a distribution on G that is invariant under conjugation, and is an eigendistribution of the center of
the universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of G, in other words an invariant eigendistribution, with eigenvalue the infinitesimal character
Infinitesimal character
In mathematics, the infinitesimal character of an irreducible representation ρ of a semisimple Lie group G on a vector space V is, roughly speaking, a mapping to scalars that encodes the process of first differentiating and then diagonalizing the representation...
of the representation π.
Harish-Chandra's regularity theorem
Harish-Chandra's regularity theorem
In mathematics, Harish-Chandra's regularity theorem, introduced by , states that every invariant eigendistribution on a semisimple Lie group, and in particular every character of an irreducible unitary representation on a Hilbert space, is given by a locally integrable function...
states that any invariant eigendistribution, and in particular any character of an irreducible unitary representation on a Hilbert space, is given by a locally integrable function
Locally integrable function
In mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.- Formal definition :...
.

