
Bloch's theorem (complex variables)
Encyclopedia
In complex analysis
, a field within mathematics, Bloch's theorem is a result that gives a lower bound on the size of the image
of a certain class of holomorphic function
s. It is named after André Bloch
.
) that includes as a subset the closed unit disk |z| ≤ 1. Suppose ƒ(0) = 0 and ƒ ′ (0) = 1. Let b(ƒ) be the supremum
of those numbers r such that there is a subregion S of the open unit disk |z| < 1 on which ƒ is injective and such that ƒ(S) contains a disk of radius r. Then b(ƒ) ≥ 1/72.
of all b(ƒ) where ƒ satisfies the hypotheses of Bloch's theorem is called Bloch's constant. Bloch's theorem tells us B ≥ 1/72, but its exact value is still unknown.
The best known bounds for B at present are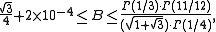
where Γ is the Gamma function
. The lower bound was proved by Chen and Gauthier, and the upper bound dates back to Ahlfors and Grunsky.
In their paper, Ahlfors and Grunsky conjectured that their upper bound is actually the true value of B.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a field within mathematics, Bloch's theorem is a result that gives a lower bound on the size of the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of a certain class of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s. It is named after André Bloch
André Bloch (mathematician)
André Bloch was a Jewish-French mathematician who is best remembered for a result called Bloch's theorem. Bloch was institutionalized in a mental asylum for thirty-one years of his life, during which all of his mathematical output was produced.- Early life :Bloch was born in 1893 in Besançon,...
.
Statement
Let ƒ be a holomorphic function on a region (i.e. an open, connected subset of CComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
) that includes as a subset the closed unit disk |z| ≤ 1. Suppose ƒ(0) = 0 and ƒ
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of those numbers r such that there is a subregion S of the open unit disk |z| < 1 on which ƒ is injective and such that ƒ(S) contains a disk of radius r. Then b(ƒ) ≥ 1/72.
Bloch's constant
The lower bound 1/72 is not the best possible. The number B defined as the infimumInfimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of all b(ƒ) where ƒ satisfies the hypotheses of Bloch's theorem is called Bloch's constant. Bloch's theorem tells us B ≥ 1/72, but its exact value is still unknown.
The best known bounds for B at present are
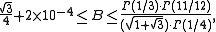
where Γ is the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. The lower bound was proved by Chen and Gauthier, and the upper bound dates back to Ahlfors and Grunsky.
In their paper, Ahlfors and Grunsky conjectured that their upper bound is actually the true value of B.

