
Bluestein's FFT algorithm
Encyclopedia
Bluestein's FFT algorithm (1968), commonly called the chirp z-transform algorithm (1969), is a fast Fourier transform
(FFT) algorithm that computes the discrete Fourier transform
(DFT) of arbitrary sizes (including prime
sizes) by re-expressing the DFT as a convolution
. (The other algorithm for FFTs of prime sizes, Rader's algorithm
, also works by rewriting the DFT as a convolution.)
In fact, Bluestein's algorithm can be used to compute more general transforms than the DFT, based on the (unilateral) z-transform
(Rabiner et al., 1969).
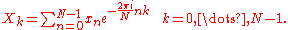
If we replace the product nk in the exponent by the identity nk = –(k–n)2/2 + n2/2 + k2/2, we thus obtain:
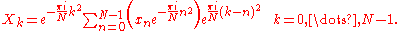
This summation is precisely a convolution of the two sequences an and bn of length N (n = 0,...,N–1) defined by:
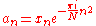
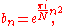
with the output of the convolution multiplied by N phase factors bk*. That is:
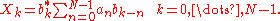
This convolution, in turn, can be performed with a pair of FFTs (plus the pre-computed FFT of bn) via the convolution theorem
. The key point is that these FFTs are not of the same length N: such a convolution can be computed exactly from FFTs only by zero-padding it to a length greater than or equal to 2N–1. In particular, one can pad to a power of two
or some other highly composite
size, for which the FFT can be efficiently performed by e.g. the Cooley–Tukey algorithm in O(N log N) time. Thus, Bluestein's algorithm provides an O(N log N) way to compute prime-size DFTs, albeit several times slower than the Cooley–Tukey algorithm for composite sizes.
The use of zero-padding for the convolution in Bluestein's algorithm deserves some additional comment. Suppose we zero-pad to a length M ≥ 2N–1. This means that an is extended to an array An of length M, where An = an for 0 ≤ n < N and An = 0 otherwise—the usual meaning of "zero-padding". However, because of the bk–n term in the convolution, both positive and negative values of n are required for bn (noting that b–n = bn). The periodic boundaries implied by the DFT of the zero-padded array mean that –n is equivalent to M–n. Thus, bn is extended to an array Bn of length M, where B0 = b0, Bn = BM–n = bn for 0 < n < N, and Bn = 0 otherwise. A and B are then FFTed, multiplied pointwise, and inverse FFTed to obtain the convolution of a and b, according to the usual convolution theorem.
Let us also be more precise about what type of convolution is required in Bluestein's algorithm for the DFT. If the sequence bn were periodic in n with period N, then it would be a cyclic convolution of length N, and the zero-padding would be for computational convenience only. However, this is not generally the case: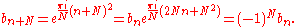
Therefore, for N even
the convolution is cyclic, but in this case N is composite
and one would normally use a more efficient FFT algorithm such as Cooley–Tukey. For N odd, however, then bn is antiperiodic and we technically have a negacyclic convolution
of length N. Such distinctions disappear when one zero-pads an to a length of at least 2N−1 as described above, however. It is perhaps easiest, therefore, to think of it as a subset of the outputs of a simple linear convolution (i.e. no conceptual "extensions" of the data, periodic or otherwise).
(Rabiner et al., 1969). In particular, it can compute any transform of the form:
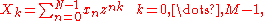
for an arbitrary complex number
z and for differing numbers N and M of inputs and outputs. Given Bluestein's algorithm, such a transform can be used, for example, to obtain a more finely spaced interpolation of some portion of the spectrum (although the frequency resolution is still limited by the total sampling time), enhance arbitrary poles in transfer-function analyses, etcetera.
The algorithm was dubbed the chirp z-transform algorithm because, for the Fourier-transform case (|z| = 1), the sequence bn from above is a complex sinusoid of linearly increasing frequency, which is called a (linear) chirp
in radar
systems.
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT) algorithm that computes the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(DFT) of arbitrary sizes (including prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
sizes) by re-expressing the DFT as a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
. (The other algorithm for FFTs of prime sizes, Rader's algorithm
Rader's FFT algorithm
Rader's algorithm is a fast Fourier transform algorithm that computes the discrete Fourier transform of prime sizes by re-expressing the DFT as a cyclic convolution...
, also works by rewriting the DFT as a convolution.)
In fact, Bluestein's algorithm can be used to compute more general transforms than the DFT, based on the (unilateral) z-transform
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
(Rabiner et al., 1969).
Algorithm
Recall that the DFT is defined by the formula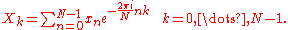
If we replace the product nk in the exponent by the identity nk = –(k–n)2/2 + n2/2 + k2/2, we thus obtain:
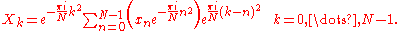
This summation is precisely a convolution of the two sequences an and bn of length N (n = 0,...,N–1) defined by:
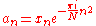
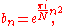
with the output of the convolution multiplied by N phase factors bk*. That is:
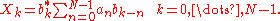
This convolution, in turn, can be performed with a pair of FFTs (plus the pre-computed FFT of bn) via the convolution theorem
Convolution theorem
In mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
. The key point is that these FFTs are not of the same length N: such a convolution can be computed exactly from FFTs only by zero-padding it to a length greater than or equal to 2N–1. In particular, one can pad to a power of two
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
or some other highly composite
Smooth number
In number theory, a smooth number is an integer which factors completely into small prime numbers. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography relying on factorization.-Definition:...
size, for which the FFT can be efficiently performed by e.g. the Cooley–Tukey algorithm in O(N log N) time. Thus, Bluestein's algorithm provides an O(N log N) way to compute prime-size DFTs, albeit several times slower than the Cooley–Tukey algorithm for composite sizes.
The use of zero-padding for the convolution in Bluestein's algorithm deserves some additional comment. Suppose we zero-pad to a length M ≥ 2N–1. This means that an is extended to an array An of length M, where An = an for 0 ≤ n < N and An = 0 otherwise—the usual meaning of "zero-padding". However, because of the bk–n term in the convolution, both positive and negative values of n are required for bn (noting that b–n = bn). The periodic boundaries implied by the DFT of the zero-padded array mean that –n is equivalent to M–n. Thus, bn is extended to an array Bn of length M, where B0 = b0, Bn = BM–n = bn for 0 < n < N, and Bn = 0 otherwise. A and B are then FFTed, multiplied pointwise, and inverse FFTed to obtain the convolution of a and b, according to the usual convolution theorem.
Let us also be more precise about what type of convolution is required in Bluestein's algorithm for the DFT. If the sequence bn were periodic in n with period N, then it would be a cyclic convolution of length N, and the zero-padding would be for computational convenience only. However, this is not generally the case:
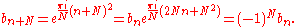
Therefore, for N even
Even and odd numbers
In mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
the convolution is cyclic, but in this case N is composite
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
and one would normally use a more efficient FFT algorithm such as Cooley–Tukey. For N odd, however, then bn is antiperiodic and we technically have a negacyclic convolution
Negacyclic convolution
In mathematics, negacyclic convolution is a convolution between two vectors a and b.It is also called skew circular convolution or wrapped convolution. It results from multiplication of a skew circulant matrix, generated by vector a, with vector b.- See also :*Circular convolution theorem...
of length N. Such distinctions disappear when one zero-pads an to a length of at least 2N−1 as described above, however. It is perhaps easiest, therefore, to think of it as a subset of the outputs of a simple linear convolution (i.e. no conceptual "extensions" of the data, periodic or otherwise).
z-Transforms
Bluestein's algorithm can also be used to compute a more general transform based on the (unilateral) z-transformZ-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
(Rabiner et al., 1969). In particular, it can compute any transform of the form:
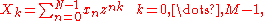
for an arbitrary complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
z and for differing numbers N and M of inputs and outputs. Given Bluestein's algorithm, such a transform can be used, for example, to obtain a more finely spaced interpolation of some portion of the spectrum (although the frequency resolution is still limited by the total sampling time), enhance arbitrary poles in transfer-function analyses, etcetera.
The algorithm was dubbed the chirp z-transform algorithm because, for the Fourier-transform case (|z| = 1), the sequence bn from above is a complex sinusoid of linearly increasing frequency, which is called a (linear) chirp
Chirp
A chirp is a signal in which the frequency increases or decreases with time. In some sources, the term chirp is used interchangeably with sweep signal. It is commonly used in sonar and radar, but has other applications, such as in spread spectrum communications...
in radar
Radar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
systems.

