
Blum-Goldwasser cryptosystem
Encyclopedia
The Blum-Goldwasser cryptosystem is an asymmetric key encryption algorithm proposed by Manuel Blum
and Shafi Goldwasser
in 1984. Blum-Goldwasser is a probabilistic
, semantically secure
cryptosystem with a constant-size ciphertext expansion
. The encryption algorithm implements an XOR-based stream cipher
using the Blum Blum Shub (BBS) pseudo-random number generator to generate the keystream
. Decryption is accomplished by manipulating the final state of the BBS generator using the secret key, in order to find the initial seed and reconstruct the keystream.
The BG cryptosystem is semantically secure
based on the assumed intractability of integer factorization
; specifically, factoring a composite value where
where  are large primes
are large primes
. BG has multiple advantages over earlier probabilistic encryption schemes such as the Goldwasser-Micali cryptosystem
. First, its semantic security reduces solely to integer factorization, without requiring any additional assumptions (e.g., hardness of the quadratic residuosity problem
or the RSA problem
). Secondly, BG is efficient in terms of storage, inducing a constant-size ciphertext expansion
regardless of message length. BG is also relatively efficient in terms of computation, and fairs well even in comparison with cryptosystems such as RSA (depending on message length and exponent choices). However, BG is highly vulnerable to adaptive chosen ciphertext attacks (see below).
Because encryption is performed using a probabilistic algorithm, a given plaintext may produce very different ciphertexts each time it is encrypted. This has significant advantages, as it prevents an adversary from recognizing intercepted messages by comparing them to a dictionary of known ciphertexts.
Blum-Goldwasser consists of three algorithms: a probabilistic key generation algorithm which produces a public and a private key, a probabilistic encryption algorithm, and a deterministic decryption algorithm.
. This value is generated in the same manner as an RSA modulus, except that the prime factors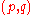 must be congruent to 3 mod 4. (See RSA, key generation for details.)
must be congruent to 3 mod 4. (See RSA, key generation for details.)
The public key is . The secret key is the factorization
. The secret key is the factorization 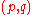 .
.
Bob sends the ciphertext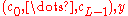 .
.
To improve performance, the BBS generator can securely output up to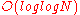 of the least-significant bits of
of the least-significant bits of 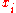 during each round. See Blum Blum Shub for details.
during each round. See Blum Blum Shub for details.
 . She can recover
. She can recover  using the following procedure:
using the following procedure:
Alice recovers the plaintext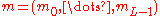 .
.
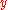 and the public key
and the public key  . However, ciphertexts of the form
. However, ciphertexts of the form 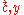 are vulnerable to an adaptive chosen ciphertext attack in which the adversary requests the decryption
are vulnerable to an adaptive chosen ciphertext attack in which the adversary requests the decryption 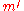 of a chosen ciphertext
of a chosen ciphertext 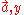 . The decryption
. The decryption  of the original ciphertext can be computed as
of the original ciphertext can be computed as  .
.
Depending on plaintext size, BG may be more or less computationally expensive than RSA. Because most RSA deployments use a fixed encryption exponent optimized to minimize encryption time, RSA encryption will typically outperform BG for all but the shortest messages. However, as the RSA decryption exponent is randomly distributed, modular exponentiation may require a comparable number of squarings/multiplications to BG decryption for a ciphertext of the same length. BG has the advantage of scaling more efficiently to longer ciphertexts, where RSA requires multiple separate encryptions. In these cases, BG may be significantly more efficient.
Manuel Blum
Manuel Blum is a computer scientist who received the Turing Award in 1995 "In recognition of his contributions to the foundations of computational complexity theory and its application to cryptography and program checking".-Biography:Blum attended MIT, where he received his bachelor's degree and...
and Shafi Goldwasser
Shafi Goldwasser
Shafrira Goldwasser is the RSA Professor of electrical engineering and computer science at MIT, and a professor of mathematical sciences at the Weizmann Institute of Science, Israel.-Biography:...
in 1984. Blum-Goldwasser is a probabilistic
Probabilistic encryption
Probabilistic encryption is the use of randomness in an encryption algorithm, so that when encrypting the same message several times it will, in general, yield different ciphertexts...
, semantically secure
Semantic security
Semantic security is a widely used definition for security in an asymmetric key encryption algorithm. For a cryptosystem to be semantically secure, it must be infeasible for a computationally bounded adversary to derive significant information about a message when given only its ciphertext and...
cryptosystem with a constant-size ciphertext expansion
Ciphertext expansion
In cryptography, the term ciphertext expansion refers to the length increase of a message when it is encrypted. Many modern cryptosystems cause some degree of expansion during the encryption process, for instance when the resulting ciphertext must include a message-unique Initialization Vector...
. The encryption algorithm implements an XOR-based stream cipher
Stream cipher
In cryptography, a stream cipher is a symmetric key cipher where plaintext digits are combined with a pseudorandom cipher digit stream . In a stream cipher the plaintext digits are encrypted one at a time, and the transformation of successive digits varies during the encryption...
using the Blum Blum Shub (BBS) pseudo-random number generator to generate the keystream
Keystream
In cryptography, a keystream is a stream of random or pseudorandom characters that are combined with a plaintext message to produce an encrypted message ....
. Decryption is accomplished by manipulating the final state of the BBS generator using the secret key, in order to find the initial seed and reconstruct the keystream.
The BG cryptosystem is semantically secure
Semantic security
Semantic security is a widely used definition for security in an asymmetric key encryption algorithm. For a cryptosystem to be semantically secure, it must be infeasible for a computationally bounded adversary to derive significant information about a message when given only its ciphertext and...
based on the assumed intractability of integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
; specifically, factoring a composite value
 where
where  are large primes
are large primesPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. BG has multiple advantages over earlier probabilistic encryption schemes such as the Goldwasser-Micali cryptosystem
Goldwasser-Micali cryptosystem
The Goldwasser–Micali cryptosystem is an asymmetric key encryption algorithm developed by Shafi Goldwasser and Silvio Micali in 1982. GM has the distinction of being the first probabilistic public-key encryption scheme which is provably secure under standard cryptographic assumptions...
. First, its semantic security reduces solely to integer factorization, without requiring any additional assumptions (e.g., hardness of the quadratic residuosity problem
Quadratic residuosity problem
The quadratic residuosity problem in computational number theory is the question of distinguishing by calculating the quadratic residues modulo N, where N is a composite number...
or the RSA problem
RSA problem
In cryptography, the RSA problem summarizes the task of performing an RSA private-key operation given only the public key. The RSA algorithm raises a message to an exponent, modulo a composite number N whose factors are not known. As such, the task can be neatly described as finding the eth roots...
). Secondly, BG is efficient in terms of storage, inducing a constant-size ciphertext expansion
Ciphertext expansion
In cryptography, the term ciphertext expansion refers to the length increase of a message when it is encrypted. Many modern cryptosystems cause some degree of expansion during the encryption process, for instance when the resulting ciphertext must include a message-unique Initialization Vector...
regardless of message length. BG is also relatively efficient in terms of computation, and fairs well even in comparison with cryptosystems such as RSA (depending on message length and exponent choices). However, BG is highly vulnerable to adaptive chosen ciphertext attacks (see below).
Because encryption is performed using a probabilistic algorithm, a given plaintext may produce very different ciphertexts each time it is encrypted. This has significant advantages, as it prevents an adversary from recognizing intercepted messages by comparing them to a dictionary of known ciphertexts.
Scheme definition
Note that the following description is a draft, and may contain errors!Blum-Goldwasser consists of three algorithms: a probabilistic key generation algorithm which produces a public and a private key, a probabilistic encryption algorithm, and a deterministic decryption algorithm.
Key generation
To allow for decryption, the modulus used in Blum-Goldwasser encryption should be a Blum integerBlum integer
In mathematics, a natural number n is a Blum integer if n = p×q is a semiprime for which p and q are distinct prime numbers congruent to 3 mod 4. That is, p and q must be of the form 4t+3, for some integer t. Primes of this form are referred to as Blum primes. This means that the factors of a Blum...
. This value is generated in the same manner as an RSA modulus, except that the prime factors
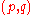 must be congruent to 3 mod 4. (See RSA, key generation for details.)
must be congruent to 3 mod 4. (See RSA, key generation for details.)- Alice generates two large prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s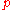 and
and 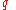 such that
such that  , randomly and independently of each other, where
, randomly and independently of each other, where 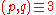 mod
mod  .
. - Alice computes
 .
.
The public key is
 . The secret key is the factorization
. The secret key is the factorization 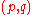 .
.Message encryption
Suppose Bob wishes to send a message m to Alice:- Bob first encodes
 as a string of
as a string of 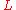 bits
bits  .
. - Bob selects a random element
 , where
, where 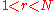 , and computes
, and computes 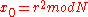 .
. - Bob uses the BBS pseudo-random number generator to generate
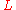 random bits
random bits  (the keystream), as follows:
(the keystream), as follows:
- For
 to
to  :
: - Set
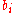 equal to the least-significant bit of
equal to the least-significant bit of 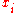 .
. - Increment
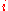 .
. - Compute
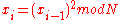 .
.
- For
- Compute the ciphertext by XORing the plaintext bits with the keystream:
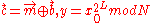 .
.
Bob sends the ciphertext
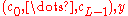 .
.To improve performance, the BBS generator can securely output up to
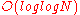 of the least-significant bits of
of the least-significant bits of 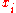 during each round. See Blum Blum Shub for details.
during each round. See Blum Blum Shub for details.Message decryption
Alice receives . She can recover
. She can recover  using the following procedure:
using the following procedure:- Using the prime factorization
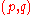 , Alice computes
, Alice computes 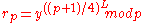 and
and  .
. - Compute the initial seed

- From
 , recompute the bit-vector
, recompute the bit-vector 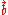 using the BBS generator, as in the encryption algorithm.
using the BBS generator, as in the encryption algorithm. - Compute the plaintext by XORing the keystream with the ciphertext:
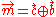 .
.
Alice recovers the plaintext
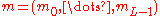 .
.Security and efficiency
The Blum-Goldwasser scheme is semantically-secure based on the hardness of predicting the keystream bits given only the final BBS state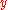 and the public key
and the public key  . However, ciphertexts of the form
. However, ciphertexts of the form 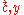 are vulnerable to an adaptive chosen ciphertext attack in which the adversary requests the decryption
are vulnerable to an adaptive chosen ciphertext attack in which the adversary requests the decryption 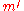 of a chosen ciphertext
of a chosen ciphertext 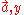 . The decryption
. The decryption  of the original ciphertext can be computed as
of the original ciphertext can be computed as  .
.Depending on plaintext size, BG may be more or less computationally expensive than RSA. Because most RSA deployments use a fixed encryption exponent optimized to minimize encryption time, RSA encryption will typically outperform BG for all but the shortest messages. However, as the RSA decryption exponent is randomly distributed, modular exponentiation may require a comparable number of squarings/multiplications to BG decryption for a ciphertext of the same length. BG has the advantage of scaling more efficiently to longer ciphertexts, where RSA requires multiple separate encryptions. In these cases, BG may be significantly more efficient.

