
Boas–Buck polynomials
Encyclopedia
In mathematics, Boas–Buck polynomials are sequences of polynomials Φ(x) given by generating function
s of the form
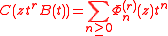 .
.
The case r=1, sometimes called generalized Appell polynomials, was studied by .
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
s of the form
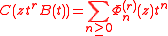 .
.The case r=1, sometimes called generalized Appell polynomials, was studied by .

