Generalized Appell polynomials
Encyclopedia
In mathematics
, a polynomial sequence
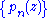has a generalized Appell representation if the generating function
for the polynomial
s takes on a certain form:
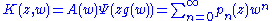
where the generating function or kernel
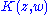is composed of the series
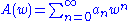with 
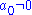
and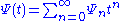
and all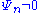 
and
with 
Given the above, it is not hard to show that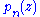
is a polynomial of degree
.
Boas–Buck polynomials are a slightly more general class of polynomials.
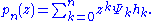
The constant is
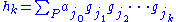
where this sum extends over all partitions
of
into 
parts; that is, the sum extends over all 
such that
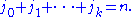
For the Appell polynomials, this becomes the formula
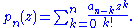
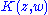can be written as 
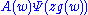with 
is that
where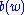
and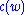 
have the power series
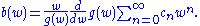
Substituting
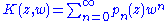
immediately gives the recursion relation
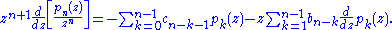
For the special case of the Brenke polynomials, one has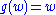
and thus all of the 
, simplifying the recursion relation significantly.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a polynomial sequence
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
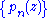has a generalized Appell representation if the generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for the polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s takes on a certain form:
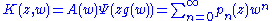
where the generating function or kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
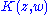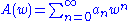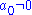
is composed of the series with and
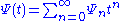and all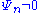 and
with Given the above, it is not hard to show that
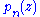is a polynomial of degreeDegree (mathematics)
In mathematics, there are several meanings of degree depending on the subject.- Unit of angle :A degree , usually denoted by ° , is a measurement of a plane angle, representing 1⁄360 of a turn...
.Boas–Buck polynomials are a slightly more general class of polynomials.
Special cases
- The choice of
gives the class of Brenke polynomials. - The choice of
results in the Sheffer sequence of polynomials, which include the general difference polynomials, such as the Newton polynomials. - The combined choice of
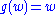and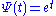 
gives the Appell sequence of polynomials.
Explicit representation
The generalized Appell polynomials have the explicit representation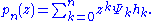The constant is
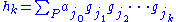
where this sum extends over all partitions
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of
into parts; that is, the sum extends over all such that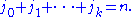For the Appell polynomials, this becomes the formula
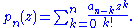
Recursion relation
Equivalently, a necessary and sufficient condition that the kernel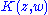 can be written as 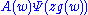with is thatwhere
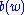and 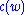have the power series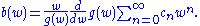Substituting
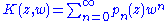
immediately gives the recursion relation
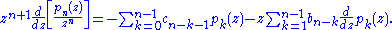
For the special case of the Brenke polynomials, one has
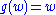and thus all of the , simplifying the recursion relation significantly.