
Bochner measurable function
Encyclopedia
In mathematics
– specifically, in functional analysis
– a Bochner-measurable function taking values in a Banach space
is a function
that equals a.e. the limit of a sequence of measurable countably-valued functions, i.e.,

where the functions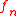 each have a countable range and for which the pre-image
each have a countable range and for which the pre-image 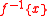 is measurable for each x. The concept is named after Salomon Bochner
is measurable for each x. The concept is named after Salomon Bochner
.
Bochner-measurable functions are sometimes called strongly measurable, -measurable or just measurable (or uniformly measurable in case that the Banach space is the space of continuous linear operators between Banach spaces).
-measurable or just measurable (or uniformly measurable in case that the Banach space is the space of continuous linear operators between Banach spaces).
In the case that B is separable, since any subset of a separable Banach space is itself separable, one can take N above to be empty, and it follows that the notions of weak and strong measurability agree when B is separable.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
– specifically, in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
– a Bochner-measurable function taking values in a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that equals a.e. the limit of a sequence of measurable countably-valued functions, i.e.,

where the functions
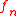 each have a countable range and for which the pre-image
each have a countable range and for which the pre-image 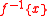 is measurable for each x. The concept is named after Salomon Bochner
is measurable for each x. The concept is named after Salomon BochnerSalomon Bochner
Salomon Bochner was an American mathematician of Austrian-Hungarian origin, known for wide-ranging work in mathematical analysis, probability theory and differential geometry.- Life :...
.
Bochner-measurable functions are sometimes called strongly measurable,
 -measurable or just measurable (or uniformly measurable in case that the Banach space is the space of continuous linear operators between Banach spaces).
-measurable or just measurable (or uniformly measurable in case that the Banach space is the space of continuous linear operators between Banach spaces).Properties
The relationship between measurability and weak measurability is given by the following result, known as Pettis' theorem or Pettis measurability theorem.
Function f is almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
separably valued (or essentially separably valued) if there exists a subset N ⊆ X with μ(N) = 0 such that f(X \ N) ⊆ B is separable.
A function : X → B defined on a measure space (X, Σ, μ) and taking values in a Banach space B is (strongly) measurable (with respect to Σ and the Borel σ-algebra on B) if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is both weakly measurable and almost surely separably valued.
In the case that B is separable, since any subset of a separable Banach space is itself separable, one can take N above to be empty, and it follows that the notions of weak and strong measurability agree when B is separable.
See also
- Bochner integralBochner integralIn mathematics, the Bochner integral, named for Salomon Bochner, extends the definition of Lebesgue integral to functions that take values in a Banach space, as the limit of integrals of simple functions.-Definition:...
- Pettis integralPettis integralIn mathematics, the Pettis integral or Gelfand–Pettis integral, named after I. M. Gelfand and B.J. Pettis, extends the definition of the Lebesgue integral to functions on a measure space which take values in a Banach space, by the use of duality. The integral was introduced by Gelfand for the...
- Bochner spaceBochner spaceIn mathematics, Bochner spaces are a generalization of the concept of Lp spaces to functions whose values lie in a Banach space which is not necessarily the space R or C of real or complex numbers....
- Measurable space
- Vector-valued measure
- Measurable functionMeasurable functionIn mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...

