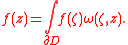Bochner–Martinelli formula
Encyclopedia
In mathematics, the Bochner–Martinelli formula is a generalization of the Cauchy integral formula to functions of several complex variables
, introduced by and .

(where the term dj is omitted).
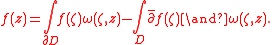
In particular if f is holomorphic the second term vanishes, so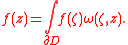
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, introduced by and .
Bochner–Martinelli kernel
For ζ, z in C n the Bochner–Martinelli kernel ω(ζ,z) is a differential form in ζ of bidegree (n,n−1) defined by
(where the term dj is omitted).
Bochner–Martinelli formula
Suppose that f is a continuously differentiable function on the closure of a domain D in Cn with piecewise smooth boundary ∂D. Then the Bochner–Martinelli formula states that if z is in the domain D then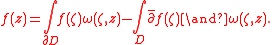
In particular if f is holomorphic the second term vanishes, so